本试题 “α是第二象限角,P(x,5)为其终边上一点,且cosα=24x,则sinα=______.” 主要考查您对象限角、轴线角
任意角的三角函数
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 象限角、轴线角
- 任意角的三角函数
象限角:
在直角坐标系中,使角的顶点与原点重合,角的始边与x轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。
轴线角:
如果角的终边在坐标轴上,就认为这个角不属于任何象限,称为轴线角。
第一、二、三、四象限角的集合分别表示为:
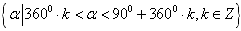 、
、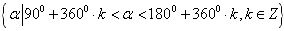 、
、 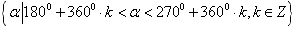 、
、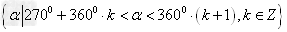 ;
;
轴线角的集合:
终边在x轴上的角的集合: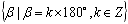 ;
;
终边在y轴上的角的集合: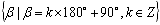 ;
;
终边在坐标轴上的角的集合: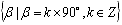 ;
;
已知α是第几象限的角,如何确定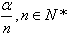 所在象限的角的常用方法:
所在象限的角的常用方法:
(1)分类讨论法,先根据α的范围用整数k把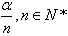 的范围表示出来,再对k分n种情况讨论;
的范围表示出来,再对k分n种情况讨论;
(2)几何法:把各象限均先n等分,再从x轴的正方向的上方起,依次将各区域标上①、②、③、④,则α原来是第几象限对应的标号即为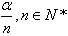 的终边所在的区域。
的终边所在的区域。
常用结论:
(1)已知α所在象限,求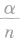
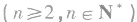 所在象限:通过分类讨论把角写成
所在象限:通过分类讨论把角写成 的形式,然后判断
的形式,然后判断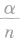 所在象限.
所在象限.
(2)由α所在象限,确定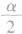 所在象限:
所在象限:
①画出区域:将坐标系每个象限二等分,得8个区域.
②标号:自x轴正向逆时针方向把每个区域依次标上I、Ⅱ、Ⅲ、Ⅳ,如图所示,
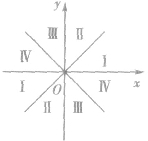
③确定区域:找出与角α所在象限标号一致的区域,即为所求.
(3)由α所在象限,确定 所在象限:
所在象限:
①画出区域:将坐标系每个象限三等分,得到12个区域.
②标号:自x轴正向逆时针方向把每个区域依次标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,如图所示,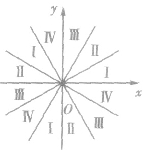
③确定区域:找出与角α所在象限标号一致的区域,即为所求.
任意角的三角函数的定义:
设α是任意一个角,α的终边上任意一点P的坐标是(x,y),它与原点的距离是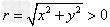 ,那么
,那么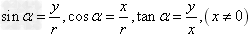 ,
,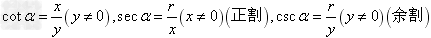 ,
,
以上以角为自变量,比值为函数的六个函数统称为三角函数。三角函数值只与角的大小有关,而与终边上点P的位置无关。
象限角的三角函数符号:
一全正,二正弦,三两切,四余弦。
特殊角的三角函数值:(见下表)
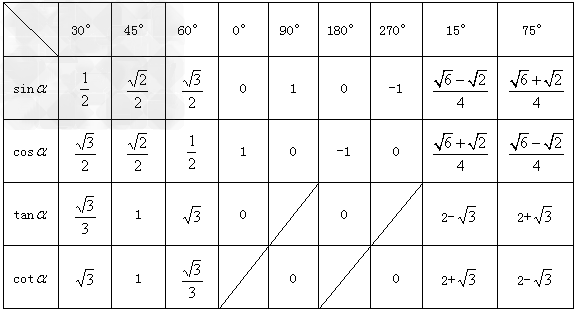
发现相似题
与“α是第二象限角,P(x,5)为其终边上一点,且cosα=24x,则sin...”考查相似的试题有:
- 已知点P(sinα•cosα,2cosα)在第四象限,则角α的终边在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限
- 函数y=2cos2x+1(x∈R)的最小正周期为______.
- 在△中,已知、、分别是三内角、、所对应的边长,且(Ⅰ)求角的大小;(Ⅱ)若,且△的面积为,求
- 函数。(1)求的周期;(2)解析式及在上的减区间;(3)若,,求的值。
- 已知向量a=(3sinωx,cosωx),b=(cosωx,-cosωx),(ω>0),函数f(x)=a•b+12的图象的两相邻对称轴间的距离为π4.(1)求ω...
- 已知函数,.(1)设是函数图像的一条对称轴,求的值;(2)求函数的单调递增区间.
- 函数y=cos2(x+π4)-sin2(x+π4)的最小正周期为( )A.π4B.π2C.πD.2π
- 函数为奇函数,且在上为减函数的值可以是( )A.B. C.D.
- 关于函数f(x)=2sin(3x-3π4),有下列命题:①最小正周期是2π3;②其图象可由y=2sin3x向右平移3π4个单位得到;③其表达式可改写为y...
- (8分)已知 ,.(Ⅰ)求的值;(Ⅱ)求的值.