返回

高中数学

首页
首页 高中数学知识 任意角的三角函数 两角和与差的三角函数及三角恒等变换 向量数量积的运算 试题正文
  • 解答题
    已知向量a=（
    		3
    sinωx，cosωx），b=（cosωx，-cosωx），（ω＞0），函数f(x)=a•b+
    1
    2
    的图象的两相邻对称轴间的距离为
    π
    4
    ．
    （1）求ω值；
    （2）若x∈(
    7
    24
    π，
    5
    12
    π)    时，f(x)=-
    3
    5
    ，求cos4x的值；
    （3）若cosx≥
    1
    2
    ，x∈（0，π），且f（x）=m有且仅有一个实根，求实数m的值．
    本题信息：2013年盐城一模数学解答题难度一般 来源:未知
  • 本题答案
    查看答案
本试题 “已知向量a=（3sinωx，cosωx），b=（cosωx，-cosωx），（ω＞0），函数f(x)=a•b+12的图象的两相邻对称轴间的距离为π4．（1）求ω值；（2）若x∈(724π，512π)时，f...” 主要考查您对

任意角的三角函数

两角和与差的三角函数及三角恒等变换

向量数量积的运算

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 任意角的三角函数
  • 两角和与差的三角函数及三角恒等变换
  • 向量数量积的运算

任意角的三角函数的定义：

设α是任意一个角，α的终边上任意一点P的坐标是（x，y），它与原点的距离是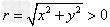，那么，，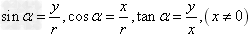
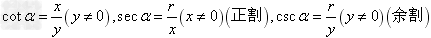以上以角为自变量，比值为函数的六个函数统称为三角函数。三角函数值只与角的大小有关，而与终边上点P的位置无关。

象限角的三角函数符号：

一全正，二正弦，三两切，四余弦。


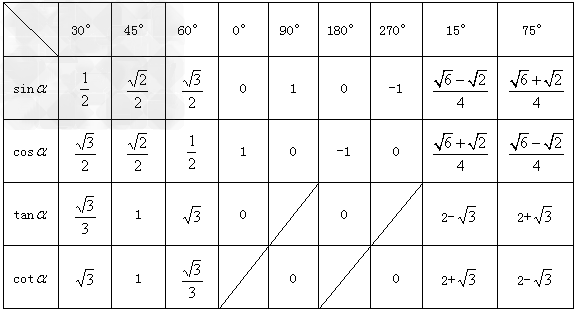
特殊角的三角函数值：（见下表）



两角和与差的公式：






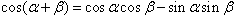
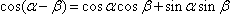
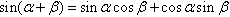
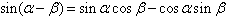
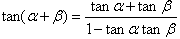
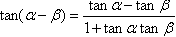
倍角公式：



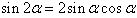
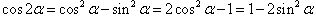
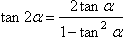
半角公式：


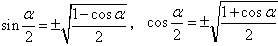
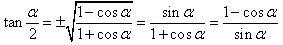
万能公式：

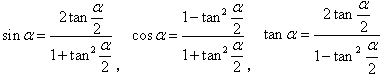
三角函数的积化和差与和差化积：








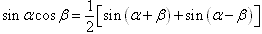
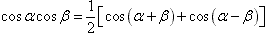
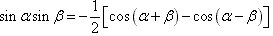
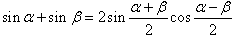
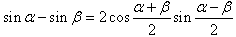
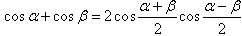
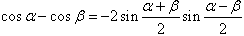
三角恒等变换：

寻找式子所包含的各个角之间的联系，并以此为依据选择可以联系它们的适当公式，这是三角恒等变换的特点。


三角函数式化简要遵循的"三看"原则:

(1)一看"角".这是最重要的一点,通过角之间的关系,把角进行合理拆分与拼凑,从而正确使用公式.
(2)二看"函数名称".看函数名称之间的差异,从而确定使用的公式.
(3)三看"结构特征".分析结构特征,可以帮助我们找到变形得方向,常见的有"遇到分式要通分"等.

方法提炼:

(1)解决给值求值问题的一般思路:
①先化简需求值得式子;②观察已知条件与所求值的式子之间的联系(从三角函数名及角入手);③将已知条件代入所求式子,化简求值.
(2)解决给值求角问题的一般步骤:
①求出角的某一个三角函数值;②确定角的范围;③根据角的范围确定所求的角.


两个向量数量积的含义：

如果两个非零向量，，它们的夹角为，我们把数量叫做与的数量积（或内积或点积），记作：，即。
叫在上的投影。
规定：零向量与任一向量的数量积是0，注意数量积是一个实数，不再是一个向量。


数量积的的运算律：

已知向量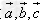和实数λ，下面（1）（2）（3）分别叫做交换律，数乘结合律，分配律。
（1）；
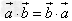（2）；
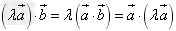（3）。


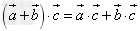向量数量积的性质：

设两个非零向量
（1）；
（2）；
（3）；
（4）；
（5）当，同向时，；当与反向时，；当为锐角时，为正且，不同向，；当为钝角时，为负且，不反向，。


发现相似题
与“已知向量a=（3sinωx，cosωx），b=（cosωx，-cosωx），（ω＞0...”考查相似的试题有：