返回

高中数学

首页
首页 高中数学知识 函数的定义域、值域 对数函数的解析式及定义（定义域、值域） 正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等） 试题正文
  • 单选题
    已知函数y=f（log2x）的定义域为[1，4]，则函数y=f（2sinx-1）的定义域是（　　）
    A．(2kπ-
    7π
    6
    ，2kπ+
    π
    6
    )          k∈Z    		B．[2kπ+
    π
    6
    ，2kπ+
    5π
    6
    ]              k∈Z
    C．[2kπ-
    2π
    3
    ，2kπ+
    π
    3
    ]              k∈Z    		D．(2kπ-
    π
    6
    ，2kπ+
    π
    6
    )          k∈Z

    本题信息：数学单选题难度一般 来源:未知
  • 本题答案
    查看答案
本试题 “已知函数y=f（log2x）的定义域为[1，4]，则函数y=f（2sinx-1）的定义域是（ ）A．(2kπ-7π6，2kπ+π6) k∈ZB．[2kπ+π6，2kπ+5π6] k∈ZC．[2kπ-2π3，2kπ+π3] k∈ZD...” 主要考查您对

函数的定义域、值域

对数函数的解析式及定义（定义域、值域）

正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等）

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 函数的定义域、值域
  • 对数函数的解析式及定义（定义域、值域）
  • 正弦、余弦函数的图象与性质（定义域、值域、单调性、奇偶性等）

定义域、值域的概念：

自变量取值范围叫做函数的定义域，函数值的集合叫做函数的值域。


1、求函数定义域的常用方法有：

（1）根据解析式要求如偶次根式的被开方大于零，分母不能为零等；
（2）根据实际问题的要求确定自变量的范围；
（3）根据相关解析式的定义域来确定所求函数自变量的范围；
（4）复合函数的定义域：如果y是u的函数，而u是x的函数，即y=f（u），u=g（x），那么y=f[g（x）]叫做函数f与g的复合函数，u叫做中间变量，设f（x）的定义域是x∈M，g（x）的定义域是x∈N，求y=f[g（x）]的定义域时，则只需求满足 的x的集合。设y=f[g（x）]的定义域为P，则  。

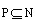 3、求函数值域的方法：

（1）利用一些常见函数的单调性和值域，如一次函数，二次函数，反比例函数，指数函数，对数函数，三角函数，形如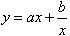 （a，b为非零常数）的函数；
（2）利用函数的图象即数形结合的方法；
（3）利用均值不等式；
（4）利用判别式；
（5）利用换元法（如三角换元）；
（6）分离法：分离常数与分离参数两种形式；
（7）利用复合函数的单调性。（注：二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系，含字母时要注意讨论）


对数函数的定义：

一般地，我们把函数y=logax（a＞0，且a≠1）叫做对数函数，其中x是自变量，函数的定义域是（0，+∞），值域是R。

对数函数的解析式：

y=logax（a＞0，且a≠1）


在解有关对数函数的解析式时注意：

在涉及到对数函数时，一定要注意定义域，即满足真数大于零；求值域时，还要考虑底数的取值范围。


正弦函数和余弦函数的图象：正弦函数y=sinx（x∈R）和余弦函数y=cosx（x∈R）的图象分别叫做正弦曲线和余弦曲线，

1．正弦函数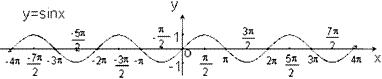

2．余弦函数

函数图像的性质
正弦、余弦函数图象的性质：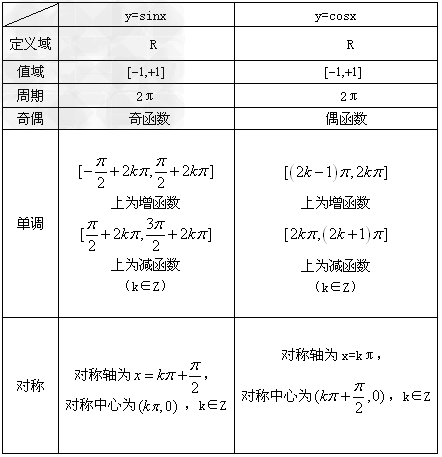

由上表知，正弦与余弦函数的定义域都是R，值域都是[-1，1]，对y=sinx，当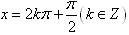时，y取最大值1，
当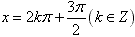时，y取最小值-1；对y=cosx，当x=2kπ（k∈Z）时，y取最大值1，当x=2kπ+π（k∈Z）时，y取最小值-1。




正弦、余弦函数图象的性质：


由上表知，正弦与余弦函数的定义域都是R，值域都是[-1，1]，对y=sinx，当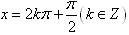时，y取最大值1，
当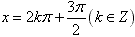时，y取最小值-1；对y=cosx，当x=2kπ（k∈Z）时，y取最大值1，当x=2kπ+π（k∈Z）时，y取最小值-1。


发现相似题
与“已知函数y=f（log2x）的定义域为[1，4]，则函数y=f（2sinx-1...”考查相似的试题有：