本试题 “已知:函数f(x)=psinωx•cosωx-cos2ωx(p>0,ω>0)的最大值为12,最小正周期为π2.(1)求:p,ω的值,f(x)的解析式;(2)若△ABC的三条边为a,b,c,满...” 主要考查您对任意角的三角函数
正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
余弦定理
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 任意角的三角函数
- 正弦、余弦函数的图象与性质(定义域、值域、单调性、奇偶性等)
- 余弦定理
任意角的三角函数的定义:
设α是任意一个角,α的终边上任意一点P的坐标是(x,y),它与原点的距离是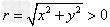 ,那么
,那么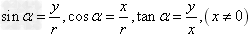 ,
,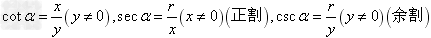 ,
,
以上以角为自变量,比值为函数的六个函数统称为三角函数。三角函数值只与角的大小有关,而与终边上点P的位置无关。
象限角的三角函数符号:
一全正,二正弦,三两切,四余弦。
特殊角的三角函数值:(见下表)
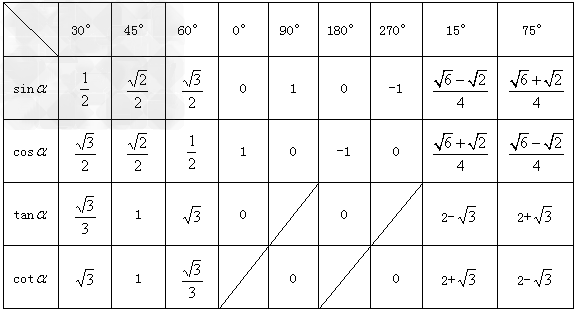
正弦函数和余弦函数的图象:正弦函数y=sinx(x∈R)和余弦函数y=cosx(x∈R)的图象分别叫做正弦曲线和余弦曲线,
1.正弦函数 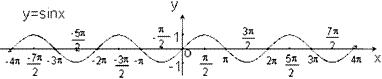
2.余弦函数
函数图像的性质
正弦、余弦函数图象的性质: 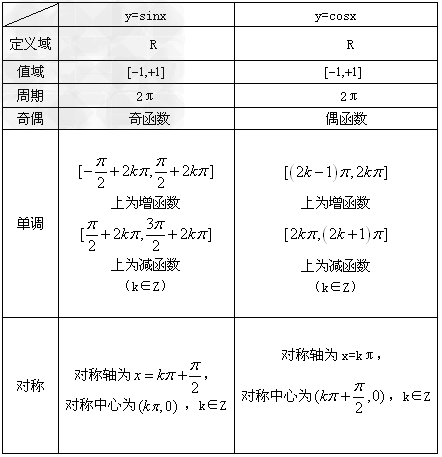
由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当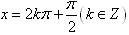 时,y取最大值1,
时,y取最大值1,
当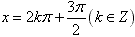 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
正弦、余弦函数图象的性质:

由上表知,正弦与余弦函数的定义域都是R,值域都是[-1,1],对y=sinx,当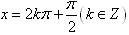 时,y取最大值1,
时,y取最大值1,
当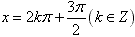 时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
时,y取最小值-1;对y=cosx,当x=2kπ(k∈Z)时,y取最大值1,当x=2kπ+π(k∈Z)时,y取最小值-1。
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: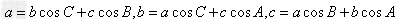
发现相似题
与“已知:函数f(x)=psinωx•cosωx-cos2ωx(p>0,ω>0)的最大...”考查相似的试题有:
- 已知函数,(1)若,求实数的解集;(2)将函数的图象向右平移个单位后,再将得到的函数图象上的各点横坐标伸长到原来的倍,...
- 已知,则等于( )A.B.C.D.
- (本小题满分10分)某港口的水深(米)是时间(,单位:小时)的函数,下面是每天时间与水深的关系表:0369121518212410139.9...
- 如图,某货轮在A处看灯塔B在货轮的北偏东,距离为海里,在A处看灯塔C在货轮的北偏西,距离为海里。货轮由A处向正北方向航行到...
- 已知函数f(x)=2cos2x2-3sinx.(Ⅰ)求函数f(x)的最小正周期和值域;(Ⅱ)若a为第二象限角,且f(a-π3)=13,求cos2a1+cos2a...
- 已知,则的值为 .
- 函数y=cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所表示,A、B分别为最高点与最低点,并且两点间的距离为...
- 函数y=-3sinx+cosx在x∈[-π6,π6]时的值域是( )A.[0,62]B.[-3,0]C.[0,1]D.[0,3]
- θ为三角形的内角,若关于x的不等式x2•cosθ-x•4sinθ+6>0恒成立,θ的取值范围是______.
- 已知函数的部分图象如下图所示,(Ⅰ)求函数f(x)的解析式;(Ⅱ)在△ABC中,角A,B,C对的边分别为a,b,c,若f(x)在x∈[4...