本试题 “已知△OPQ的面积为S,且;(1)若,求向量与的夹角θ的取值范围;(2)设=m,S=m,以O为中心,P为焦点的椭圆经过点Q,当m在[2,+∞)上变动时,求的最小值,并求...” 主要考查您对函数的单调性、最值
面积定理:S=1/2absinC=1/2acsinB=1/2bcsinA
向量模的计算
椭圆的标准方程及图象
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的单调性、最值
- 面积定理:S=1/2absinC=1/2acsinB=1/2bcsinA
- 向量模的计算
- 椭圆的标准方程及图象
单调性的定义:
1、对于给定区间D上的函数f(x),若对于任意x1,x2∈D,当x1<x2时,都有f(x1)<f(x2),则称f(x)是区间上的增函数;当x1<x2时,都有f(x1)>f(x2),则称f(x)是区间D上的减函数。
2、如果函数y=f(x)在区间上是增函数或减函数,就说函数y=f(x)在区间D上具有(严格的)单调性,区间D称为函数f(x)的单调区间。如果函数y=f(x)在区间D上是增函数或减函数,区间D称为函数f(x)的单调增或减区间
3、最值的定义:
最大值:一般地,设函数y=f(x)的定义域为I,如果存在实数M,满足: ①对于任意的x∈I,都有f(x)≤M;②存在x0∈I,使得f(x0)=M;那么,称M是f(x)的最大值.
最小值:一般地,设函数y=f(x)的定义域为I,如果存在实数M,满足: ①对于任意的x∈I,都有f(x)≥M;②存在x0∈I,使得f(x0)=M;那么,称M是f(x)的最小值
判断函数f(x)在区间D上的单调性的方法:
(1)定义法:其步骤是:
①任取x1,x2∈D,且x1<x2;
②作差f(x1)-f(x2)或作商 ,并变形;
,并变形;
③判定f(x1)-f(x2)的符号,或比较 与1的大小;
与1的大小;
④根据定义作出结论。
(2)复合法:利用基本函数的单调性的复合。
(3)图象法:即观察函数在区间D上部分的图象从左往右看是上升的还是下降的。
三角形面积公式:
(1)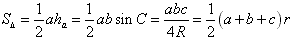
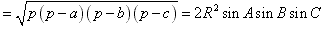 ,
,
其中r为三角形ABC内切圆半径,R为外接圆的半径, 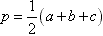 。
。
(2)数量积形式的三角形面积公式:
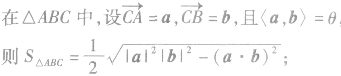
(3)坐标形式的三角形面积公式:

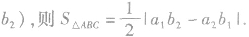
方法提炼:
(1)三角形的面积经常与正余弦定理结合在一起考查,解题时要注意方程思想的运用,即通过正余弦定理建立起方程(组),进而求得边或角;
(2)要熟记常用的面积公式及其变形.
向量的模:
设 ,则有向线段
,则有向线段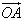 的长度叫做向量
的长度叫做向量 的长度或模,记作:
的长度或模,记作: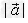 ,则
,则  。
。
向量模的坐标表示:
(1)若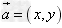 ,则
,则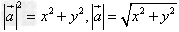 ;
;
(2)若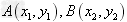 ,那么
,那么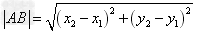 。
。
求向量的模:
求向量的模主要是利用公式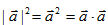 来解。
来解。
椭圆的标准方程:
(1)中心在原点,焦点在x轴上: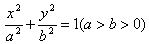 ;
;
(2)中心在原点,焦点在y轴上: 。
。
椭圆的图像:
(1)焦点在x轴: ;
;
(2)焦点在y轴: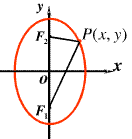 。
。
巧记椭圆标准方程的形式:
①椭圆标准方程的形式:左边是两个分式的平方和,右边是1;
②椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪一个轴上;
③椭圆的标准方程中,三个参数a,b,c满足a2= b2+ c2;
④由椭圆的标准方程可以求出三个参数a,b,c的值.
待定系数法求椭圆的标准方程:
求椭圆的标准方程常用待定系数法,要恰当地选择方程的形式,如果不能确定焦点的位置,那么有两种方法来解决问题:一是分类讨论,全面考虑问题;二是可把椭圆的方程设为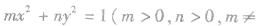 n)用待定系数法求出m,n的值,从而求出标准方程,
n)用待定系数法求出m,n的值,从而求出标准方程,
与“已知△OPQ的面积为S,且;(1)若,求向量与的夹角θ的取值范围...”考查相似的试题有:
- (本题满分12分)已知函数是奇函数,①求实数a和b的值;②判断函数在的单调性,并利用定义加以证明
- 已知△ABC的面积为1,点D在AC上,DE∥AB,连接BD,设△DCE、△ABD、△BDE中面积最大者的值为y,则y的最小值为______.
- 若,则;
- 函数f(x)=log15(x2-8x+7)的单调递减区间为______.
- 设f(x)是R上的奇函数,且f(-1)=0,当x>0时,(x2+1)f′(x)+2xf(x)<0,则不等式f(x)>0的解集为( )。
- 已知f(x)=x2+x+1,则f(2)=______;f[f(2)]=______.
- f(x)=lnx,x≥1(x-1)2,x<1,若f(x)=1,则x=______.
- 已知函数是上的增函数,(1)若,且,求证(2)判断(1)中命题的逆命题是否成立,并证明你的结论。
- 椭圆的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为,倾斜角为45°的直线l过点F.(Ⅰ)求该椭圆的方程;(Ⅱ...
- 2<m<6是方程表示椭圆的( )条件. A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要