本试题 “已知a>1,λ>0,求证:loga(a+λ)>loga+λ(a+2λ).” 主要考查您对对数与对数运算
对数函数的解析式及定义(定义域、值域)
对数函数的图象与性质
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 对数与对数运算
- 对数函数的解析式及定义(定义域、值域)
- 对数函数的图象与性质
对数的定义:
如果ax=N(a>0,且a≠1),那么数x叫做以a为底N的对数,记做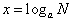 ,其中a叫做对数的底数,N叫做真数。
,其中a叫做对数的底数,N叫做真数。
通常以10为底的对数叫做常用对数,记做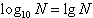 ;
;
以无理数e=2.71828…为底的对数叫做自然对数,记做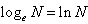 。
。
由定义知负数和0没有对数。
常用对数:
以10为底的对数叫做常用对数, 。
。
自然对数:
以e为底的对数叫做自然对数,e是无理数,e≈-2. 718 28, 。
。
对数的运算性质:
如果a>0,且a≠1,M>0,N>0,那么
(1)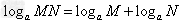 ;
;
(2)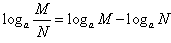 ;
;
(3) ;
;
(4) 。
。
对数的恒等式:
(1)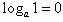 ;(2)
;(2)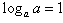 ;
;
(3)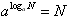 ;(4)
;(4) ;
;
(5)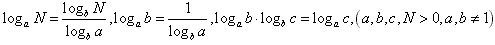 。
。
对数的换底公式及其推论:
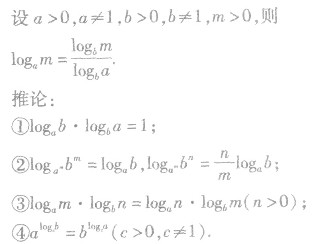
对数式的化简与求值:
(1)化同底是对数式变形的首选方向,其中经常用到换底公式及其推论.
(2)结合对数定义,适时进行对数式与指数式的互化.
(3)利用对数运算法则,在积、商、幂的对数与对数的和、差、倍之间进行转化,
对数函数的定义:
一般地,我们把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞),值域是R。
对数函数的解析式:
y=logax(a>0,且a≠1)
在解有关对数函数的解析式时注意:
在涉及到对数函数时,一定要注意定义域,即满足真数大于零;求值域时,还要考虑底数的取值范围。
对数函数的图形:
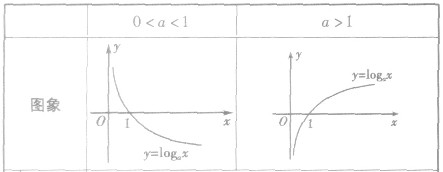
对数函数的图象与性质:
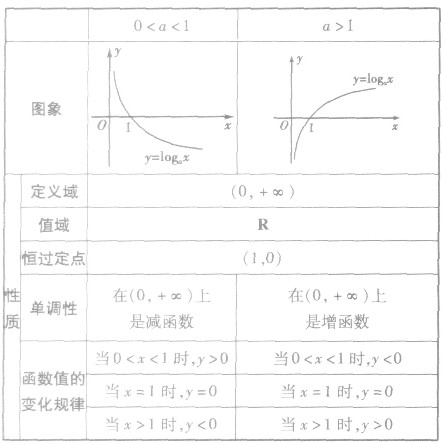
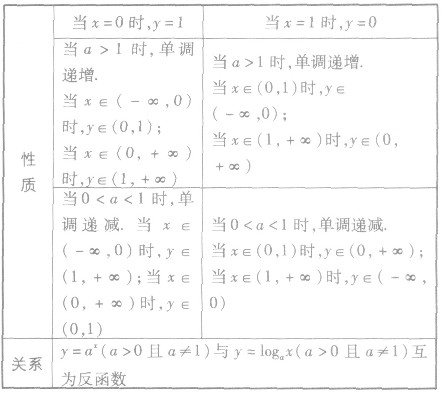
对数函数与指数函数的对比:
(1)对数函数与指数函数互为反函数,它们的定义域、值域互换,图象关于直线y=x对称.
(2)它们都是单调函数,都不具有奇偶性.当a>l时,它们是增函数;当O<a<l时,它们是减函数.
(3)指数函数与对数函数的联系与区别: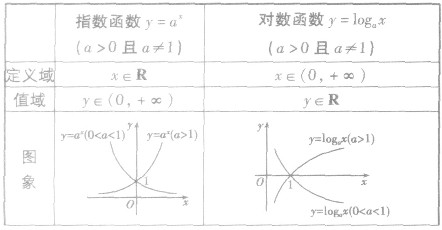
对数函数单调性的讨论:
解决与对数函数有关的函数单调性问题的关键:一是看底数是否大于l,当底数未明确给出时,则应对底数a是否大于1进行讨论;二是运用复合法来判断其单调性,但应注意中间变量的取值范围;三要注意其定义域(这是一个隐形陷阱),也就是要坚持“定义域优先”的原则.
利用对数函数的图象解题:
涉及对数型函数的图象时,一般从最基本的对数函数的图象人手,通过平移、伸缩、对称变换得到对数型函数的图象,特别地,要注意底数a>l与O<a<l的两种不同情况,
底数对函数值大小的影响:
1.在同一坐标系中分别作出函数
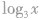 的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
的图象,如图所示,可以看出:当a>l时,底数越大,图象越靠近x轴,同理,当O<a<l时,底数越小,函数图象越靠近x轴.利用这一规律,我们可以解决真数相同、对数不等时判断底数大小的问题.
2.类似地,在同一坐标系中分别作出
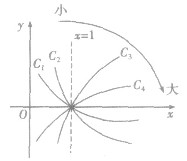
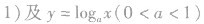 的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如
的图象,如图所示,它们的图象在第一象限的规律是:直线x=l把第一象限分成两个区域,每个区域里对数函数的底数都是由右向左逐渐减小,比如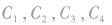 分别对应函数
分别对应函数
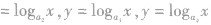 ,则必有
,则必有
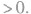
与“已知a>1,λ>0,求证:loga(a+λ)>loga+λ(a+2λ).”考查相似的试题有:
- 若,则下列结论中不正确的是[ ]A.B.C.D.
- 用二分法求函数的一个零点,其参考数据如下:f(2)≈-0.699f(3) ≈0.477f(2.5) ≈-0.102f(2.75) ≈0.189f(2.625) ≈0.044f(2.5625)≈...
- 设a>0且a≠1, (x≥1)(Ⅰ)求函数f(x)的反函数f-1(x)及其定义域;(Ⅱ)若,求a的取值范围
- 计算下列各式的值:(1);(2)。
- 下列几个命题:①函数f(x)=x2+(a-3)x+a有两个零点,一个比0大,一个比0小,则a<0;②函数y=x2-1+1-x2是偶函数,但不是奇函...
- 把函数y=logax(a>0且a≠1)的图象绕原点逆时针旋转90°后新图象的函数解析式是( )A.y=-axB.y=a-xC.y=loga(-x)D.y=-logax
- 已知函数f(x)=log3(ax+b)的图象经过点A(2,1)和B(5,2),记an=3f(n),n∈N*.(1)求数列{an}的通项公式;(2)设bn...
- 已知f(x)=log3x.(1)作出这个函数的图象;(2)当0<a<2时,利用图象判断是否有满足f(a)>f(2)的a值.
- 已知集合A={x|log3(x-1)<2},B={x|(13)x>3}则A∩CRB=______.
- 设,则A.0B.1C.2D.3