返回

高中数学

首页
首页 高中数学知识 等差数列的定义及性质 数列的极限 数列求和的其他方法（倒序相加，错位相减，裂项相加等） 数学归纳法 试题正文
  • 解答题
    数列{an}各项均为正数，Sn为其前n项的和．对于n∈N*，总有an，Sn，an2成等差数列．
    （1）求数列{an}的通项an；
    （2）设数列{
    1
    an
    }    的前n项和为Tn，数列{Tn}的前n项和为Rn，求证：当n≥2，n∈N时，Rn-1=n（Tn-1）；
    （3）若函数f(x)=
    1
    (p-1)•3qx+1
    的定义域为Rn，并且
    lim
    n→∞
    f(an)=0(n∈N*)    ，求证p+q＞1．
    本题信息：2008年南汇区二模数学解答题难度较难 来源:未知
  • 本题答案
    查看答案
本试题 “数列{an}各项均为正数，Sn为其前n项的和．对于n∈N*，总有an，Sn，an2成等差数列．（1）求数列{an}的通项an；（2）设数列{1an}的前n项和为Tn，数列{Tn}的前n项...” 主要考查您对

等差数列的定义及性质

数列的极限

数列求和的其他方法（倒序相加，错位相减，裂项相加等）

数学归纳法

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 等差数列的定义及性质
  • 数列的极限
  • 数列求和的其他方法（倒序相加，错位相减，裂项相加等）
  • 数学归纳法

等差数列的定义：

一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做公差，用符号语言表示为an+1-an=d。


等差数列的性质：

（1）若公差d＞0，则为递增等差数列；若公差d＜0，则为递减等差数列；若公差d＝0，则为常数列；
（2）有穷等差数列中，与首末两端“等距离”的两项和相等，并且等于首末两项之和；
（3）m，n∈N*，则am＝an+(m-n)d；
（4）若s，t，p，q∈N*，且s+t=p+q，则as+at=ap+aq，其中as，at，ap，aq是数列中的项，特别地，当s+t=2p时，有as+at=2ap；
（5）若数列｛an｝，｛bn｝均是等差数列，则数列｛man+kbn｝仍为等差数列，其中m，k均为常数。
（6）
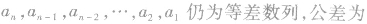
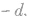
（7）从第二项开始起，每一项是与它相邻两项的等差中项，也是与它等距离的前后两项的等差中项，即
（8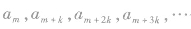） 仍为等差数列，公差为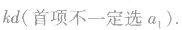


 


对等差数列定义的理解：

①如果一个数列不是从第2项起，而是从第3项或某一项起，每一项与它前一项的差是同一个常数，那么此数列不是等差数列，但可以说从第2项或某项开始是等差数列． 
②求公差d时，因为d是这个数列的后一项与前一项的差，故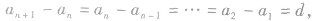有 还有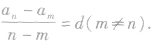
③公差d∈R，当d=0时，数列为常数列（也是等差数列）；当d>0时，数列为递增数列；当d<0时，数列为递减数列；
④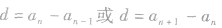 是证明或判断一个数列是否为等差数列的依据；
⑤证明一个数列是等差数列，只需证明an+1-an是一个与n无关的常数即可。

等差数列求解与证明的基本方法：

(1)学会运用函数与方程思想解题；
(2)抓住首项与公差是解决等差数列问题的关键；
(3)等差数列的通项公式、前n项和公式涉及五个量：a1，d，n，an，Sn，知道其中任意三个就可以列方程组求出另外两个(俗称“知三求二’)．


数列的极限定义（描述性的）：

如果当项数n无限增大时，无穷数列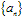的项an无限地趋近于某个常数a（即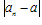无限地接近于0），a叫数列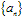的极限，记作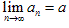，也可记做当n→+∞时，an→a。

数列的极限严格定义：

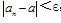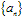即ε－N定义：对于任何正数ε（不论它多么小），总存在某正数N，使得当n＞N时，一切an都满足，a叫数列的极限。

数列极限的四则运算法则：

若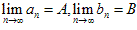，则
（1），；
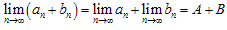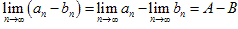（2），；
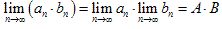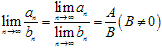（3）。
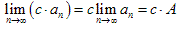前提条件：（1）各数列均有极限，（2）相加减时必须是有限个数列才能用法则。


an无限接近于a的方式有三种：

第一种是递增的数列，an无限接近于a，即an是在常数a的左边无限地趋近于a，如n→+∞时，；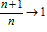
第二种是递减数列，an无限地趋近于a，即an是在常数a的右边无限地趋近于a，如n→+∞时，是；
第三种是摆动数列，an无限地趋近于a，即an是在无限摆动的过程中无限地趋近于a，如n→+∞时，。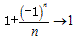


一些常用数列的极限：

（1）常数列A，A，A，…的极限是A；
（2）当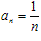时，；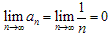
（3）当|q|＜1时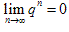，；当q＞1时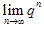，不存在；
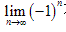（4）不存在，。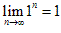
（5）无穷等比数列{an}中，首项a1，公比q，前n项和Sn，各项之和S，则（只有在0＜|q|＜1时）。


数列求和的常用方法：

1.裂项相加法：数列中的项形如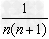的形式，可以把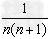表示为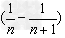，累加时抵消中间的许多项，从而求得数列的和；
2、错位相减法：源于等比数列前n项和公式的推导，对于形如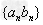的数列，其中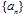为等差数列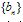，为等比数列，均可用此法；
3、倒序相加法：此方法源于等差数列前n项和公式的推导，目的在于利用与首末两项等距离的两项相加有公因式可提取，以便化简后求和。
4、分组转化法：把数列的每一项分成两项，或把数列的项“集”在一块重新组合，或把整个数列分成两个部分，使其转化为等差或等比数列，这一求和方法称为分组转化法。
5、公式法求和：所给数列的通项是关于n的多项式，此时求和可采用公式求和，常用的公式有：
 
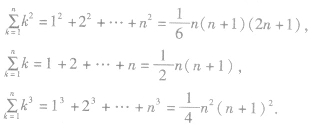
数列求和的方法多种多样，要视具体情形选用合适方法。


数列求和特别提醒：

（1）对通项公式含有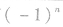的一类数列，在求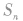时，要注意讨论n的奇偶性；
（2）在用等比数列前n项和公式时，一定要分q=1和q≠1两种情况来讨论。

 

归纳法：

对于某类事物，由它的一些特殊事例或其全部可能情况，归纳出一般结论的推理方法叫做归纳法。归纳法包括完全归纳法和不完全归纳法。

数学归纳法：

一般地，证明一个与正整数n有关的命题，可按下列步骤进行：
（1）证明当n取第一个值n0（n0∈N*）时命题成立；
（2）假设当n=k（k∈N*，k≥n0）时命题成立，证明当n=k+1时命题也成立；
完成这两步，就可以断定这个命题对从n0开始的所有正整数n都成立，这种证明方法叫做数学归纳法。


数学归纳法的特点:

①用数学归纳法进行证明时，要分两个步骤，两步同样重要，两步骤缺一不可；
②第二步证明，由假设n＝k时命题成立，到n=k+1时．必须用假设条件，否则不是数学归纳法；
③最后一定要写“由（1）（2）……”。

数学归纳法的应用：

（1）证明恒等式；
（2）证明不等式；
（3）三角函数；
（4）计算、猜想、证明。


发现相似题
与“数列{an}各项均为正数，Sn为其前n项的和．对于n∈N*，总有an，...”考查相似的试题有：