本试题 “在直角坐标系xOy中,以O为圆心的圆与直线x-y=4相切,(Ⅰ)求圆O的方程;(Ⅱ)圆O与x轴相交于A、B两点,圆内的动点P使|PA|、|PO|、|PB|成等比数列,求的取值范...” 主要考查您对等比中项
用坐标表示向量的数量积
圆的标准方程与一般方程
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等比中项
- 用坐标表示向量的数量积
- 圆的标准方程与一般方程
等比中项:
若数a,G,b成等比数列,那么就称G为a与b的等比中项,从而有G2=ab或G=±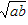 。
。
等比中项的理解:
如果a,G,b三个数成等比数列,则有G2=ab.反之不一定成立.由等比中项定义可知: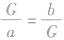 ,
, 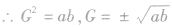 ,
,
这表明,只有同号的两项才有等比中项,并且这两项有2个互为相反数的等比中项,当a>0,b>0时,G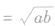 又叫做a,b的几何平均数。
又叫做a,b的几何平均数。
两个向量的数量积的坐标运算:
非零向量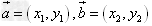 ,那么
,那么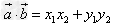 ,即两个向量的数量积等于它们对应坐标的乘积。
,即两个向量的数量积等于它们对应坐标的乘积。
向量的数量积的推广1:
设a=(x,y),则|a| =x2+y2 ,或|a|=
=x2+y2 ,或|a|=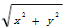
向量的数量积的推广2:
设 ,则
,则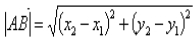
 ,则
,则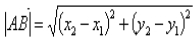
向量的数量积的坐标表示的证明:
已知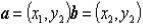 ,则
,则
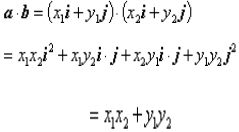
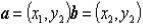 ,则
,则
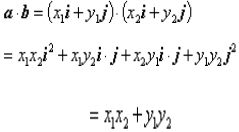
圆的定义:
平面内与一定点的距离等于定长的点的集合是圆。定点就是圆心,定长就是半径。
圆的标准方程:
圆的标准方程 ,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为
,圆心(a,b),半径为r;特别当圆心是(0,0),半径为r时,圆的标准方程为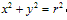 。
。
圆的一般方程:
圆的一般方程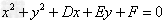
当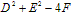 >0时,表示圆心在
>0时,表示圆心在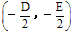 ,半径为
,半径为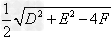 的圆;
的圆;
当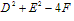 =0时,表示点
=0时,表示点 ;
;
当 <0时,不表示任何图形。
<0时,不表示任何图形。
圆的定义的理解:
(1)定位条件:圆心;定形条件:半径。
(2)当圆心位置与半径大小确定后,圆就唯一确定了.因此一个圆最基本的要素是圆心和半径.
圆的方程的理解:
(1)圆的标准方程中含有a,b,r三个独立的系数,因此,确定一个圆需三个独立的条件.其中圆心是圆的定位条件,半径是圆的定形条件.
(2)圆的标准方程的优点在于明确显示了圆心和半径.
(3)圆的一般方程形式的特点:
a.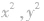 的系数相同且不等于零;
的系数相同且不等于零;
b.不含xy项.
(4)形如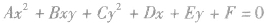 的方程表示圆的条件:
的方程表示圆的条件:
a.A=C≠0;
b.B=0;
c. 即
即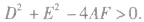
几种特殊位置的圆的方程:
| 条件 | 标准方程 | 一般方程 |
| 圆心在原点 |
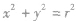 |
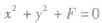 |
| 过原点 |
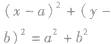 |
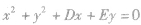 |
| 圆心在x轴上 |
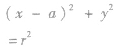 |
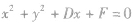 |
| 圆心在y轴上 |
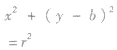 |
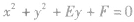 |
| 与x轴相切 |
 |
 |
| 与y轴相切 |
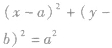 |
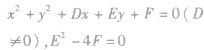 |
|
与x,y轴都相切 |
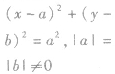 |
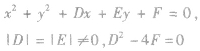 |
| 圆心在x轴上且过原点 |
 |
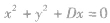 |
| 圆心在y轴上且过原点 |
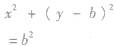 |
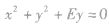 |
发现相似题
与“在直角坐标系xOy中,以O为圆心的圆与直线x-y=4相切,(Ⅰ)求...”考查相似的试题有:
- 已知向量a=(sinx,1),b=(cosx,12)(1)当a⊥b时,求|a+b|的值;(2)求函数f(x)=a-(2b-a)+cos2x的单调增区间.
- 直线ax+by+c=0与圆x2+y2=9相交于两点M,N,若c2=a2+b2,则(O为坐标原点)等于A.-7B.-14C.7D.14
- 已知向量a=(sinθ,cosθ),b=(1,-2),且a·b=0,(1)求tanθ的值;(2)求函数f(x)=cos2x+tanθsinx(x∈R)的值域。
- 已知|a|=3,|b|=4,a,b的夹角为60°,则|2a-b |=______.
- 已知均为单位向量,且=,则,的夹角为( ) A. B. C. D.
- 以两点A(-3,-1)和B(5,5)为直径端点的圆的方程是 ( ) A. B. C. D.
- (本小题满分12分)如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在的平面和圆O所在的平面垂直,且.⑴求证:;⑵设FC...
- 设集合M={(x,y)|x2+y2=1,x,y∈R},N={x|x2-y=0,x,y∈R},则M∩N中元素的个数是( )A.0B.1C.2D.3
- 设椭圆方程为,过点M(0,1)的直线l交椭圆于A,B两点,O为坐标原点,点P满足,点N的坐标为,当直线l绕点M旋转时,求:(1)动点P...
- 已知可行域的外接圆C与x轴交于点A1、A2,椭圆C1以线段A1A2为长轴,离心率.(1)求圆C及椭圆C1的方程;(2)设椭圆C1的右焦点...