本试题 “下列有关命题的说法正确的是[ ]A.命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”B.命题“若x=y,则sinx=siny”的逆否命题为真命题C.命题“存在x∈R,使得x2+x+1” 主要考查您对真命题、假命题
四种命题及其相互关系
充分条件与必要条件
全称量词与存在性量词
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 真命题、假命题
- 四种命题及其相互关系
- 充分条件与必要条件
- 全称量词与存在性量词
命题的概念:
1、命题:把语言、符号或式子表达的,可以判断真假的陈述句称为命题;
2、真命题、假命题:判断为真的语句称为真命题,判断为假的语句称为假命题。
注意:
1、并不是所有的语句都是命题,只有能够判断真假的语句才是命题。
2、如果一个语句是命题,则它是真命题或是假命题,二者必具其一。
1、四种命题:
一般地,用p和q分别表示原命题的条件和结论,用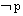 或
或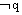 分别表示p和q的否定,
分别表示p和q的否定,
四种命题的形式是:
(1)原命题:若p则q;
(2)逆命题:若q则p;
(3)否命题:若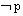 则
则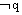 ;
;
(4)逆否命题:若 则
则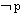 。
。
2、四种命题的真假关系:
一个命题与它的逆否命题是等价的,其逆命题与它的否命题也是等价的;
3、四种命题的相互关系:
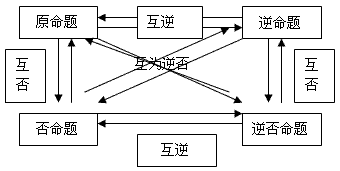
注意:
1、区别“否命题”与“命题的否定”,若原命题是“若p则q”,则这个命题的否定是“若p则非q”,而它的否命题是“若非p则非q”。
2、互为逆否命题同真假,即“等价”
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有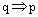 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且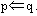 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
1、全称量词与全称命题:
①全称量词:短语“对所有的”,“对任意的”在陈述中表示整体或全部的含义,逻辑中通常叫做全称量词,并用符号“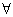 ”表示;
”表示;
②全称命题:含有全称量词的命题,叫做全称命题
③全称命题的格式:“对M中任意一个x,有p(x)成立”的命题,记为?x∈M,p(x),读作“对任意x属于M,有p(x)成立”。
2、存在量词与特称命题:
①存在量词:短语“存在一个”,“至少有一个”在陈述中表示个别或者一部分的含义,在逻辑中通常叫做存在量词,并用符号“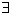 ”表示。
”表示。
②特称命题:含有存在量词的命题,叫做特称命题;
③“存在M中的一个x0,使p(x0)成立”的命题,记为?x0∈M,p(x0),读作“存在一个x0属于M,使p(x0)成立”。
3、全称命题的否定:
一般地,对于含有一个量词的全称命题的否定,有下面的结论:
全称命题p: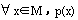 ,它的否命题
,它的否命题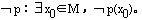
4、特称命题的否定:
一般地,对于含有一个量词的特称命题的否定,有下面的结论:
特称命题p: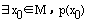 ,其否定命题
,其否定命题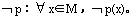
与“下列有关命题的说法正确的是[ ]A.命题“若x2=1,则x=1”的否命...”考查相似的试题有:
- 设l,m,n表示三条直线,α,β,γ表示三个平面,给出下列四个命题:①若l ⊥α,m⊥α,则l∥m;②若mβ,n是l在β内的射影,m⊥l,则m⊥n...
- 设c∈R,函数f(x)=x2-2x+c.关于函数f(x)的下述四个命题中,真命题为( )A.f(0)>f(2)B.f(0)<f(2)C.f(x)≥c...
- 已知直线及平面,下列命题中的假命题是 ( )A.若,,则B.若,,则C.若,,则D.若,,则
- 已知命题“”是假命题,则实数的取值范围是____ ____;
- 设f(x)=sin(ωx+ψ),其中ψ>0,则函数f(x)是偶函数的充分必要条件是[ ]A.f(0)=0B.f(0)=1C.f′(0)=1D.f′(0)=0
- 已知m,n是不同的直线,α,β是不同的平面,则“n⊥α”的一个充分不必要条件是[ ]A.α∥β,n⊥βB.α⊥β,nβC.α⊥β,n∥βD.m∥α,n⊥m
- “b2=ac”是“a,b,c成等比数列”的[ ]A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件
- 已知命题p:不等式|x-1|+|x+2|>m的解集为R;命题q:f(x)=log(5-2m)x为减函数.则p是q成立的( )A.充分不必要条件B.必...
- 若a、b、c是实数,则“ac<0”是“不等式ax2+bx+c>0有解”的[ ]A.充要条件B.充分不必要条件C.必要而不充分条件D.既不充分也不必...
- 下列说法正确的是( )A.函数y=2sin(2x-π6)的图象的一条对称轴是直线x=π12B.若命题p:“存在x∈R,x2-x-1>0”,则命题p的否...