本试题 “如图,直线 l1:y=kx+1-k(k≠0,k≠±)与l2:相交于点P,直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作...” 主要考查您对一般数列的通项公式
直线的方程
两条直线的交点坐标
两点间的距离
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 一般数列的通项公式
- 直线的方程
- 两条直线的交点坐标
- 两点间的距离
一般数列的定义:
如果数列{an}的第n项an与序号n之间的关系可以用一个式子表示成an=f(n),那么这个公式叫做这个数列的通项公式。
通项公式的求法:
(1)构造等比数列:凡是出现关于后项和前项的一次递推式都可以构造等比数列求通项公式;
(2)构造等差数列:递推式不能构造等比数列时,构造等差数列;
(3)递推:即按照后项和前项的对应规律,再往前项推写对应式。
已知递推公式求通项常见方法:
①已知a1=a,an+1=qan+b,求an时,利用待定系数法求解,其关键是确定待定系数λ,使an+1 +λ=q(an+λ)进而得到λ。
②已知a1=a,an=an-1+f(n)(n≥2),求an时,利用累加法求解,即an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)的方法。
③已知a1=a,an=f(n)an-1(n≥2),求an时,利用累乘法求解。
直线方程的定义:
以一个方程的解为坐标的点都是某条直线上的点,这个方程就叫做这条直线的方程,这条直线叫做这个方程的直线。
基本的思想和方法:
求直线方程是解析几何常见的问题之一,恰当选择方程的形式是每一步,然后釆用待定系数法确定方程,在求直线方程时,要注意斜率是否存在,利用截距式时,不能忽视截距为0的情形,同时要区分“截距”和“距离”。
直线方程的几种形式:
1.点斜式方程:
(1)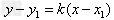 ,(直线l过点
,(直线l过点 ,且斜率为k)。
,且斜率为k)。
(2)当直线的斜率为0°时,k=0,直线的方程是y=y1。当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示,但因l上每一点的横坐标都等于x1,所以它的方程是x=x1。
2.斜截式方程:已知直线在y轴上的截距为b和斜率k,则直线的方程为:y=kx+b,它不包括垂直于x轴的直线。
3.两点式方程:已知直线经过(x1,y1),(x2,y2)两点,则直线方程为:
4.截距式方程:已知直线在x轴和y轴上的截距为a,b,则直线方程为: (a、b≠0)。
(a、b≠0)。
5.一般式方程:(1)定义:任何直线均可写成:Ax+By+C=0(A,B不同时为0)的形式。(2)特殊的方程如:平行于x轴的直线:y=b(b为常数);平行于y轴的直线:x=a(a为常数)。
几种特殊位置的直线方程:

(2)待定系数法:先设出直线的方程,再根据已知条件求出假设系数,最后代入直线方程,待定系数法常适用于斜截式,已知两点坐标等.
利用待定系数法求直线方程的步骤:①设方程;②求系数;③代入方程得直线方程,如果已知直线过一个定点
 ,可以利用直线的点斜式
,可以利用直线的点斜式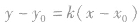 求方程,也可以利用斜截式、截距式等形式求解.
求方程,也可以利用斜截式、截距式等形式求解.两条直线的交点:
两直线: ,
,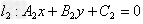 ,当它们相交时,方程组
,当它们相交时,方程组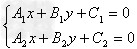 有唯一的解,以这个解为坐标的点就是两直线的交点。
有唯一的解,以这个解为坐标的点就是两直线的交点。
若方程组无解,两直线平行;若方程组有无数个解,则两直线重合。
两条直线的交点特别提醒:
①若方程组无解,则直线 平行;反之,亦成立;
平行;反之,亦成立;
②若方程组有无穷多解,则直线 重合;反之,也成立;
重合;反之,也成立;
③当有交点时,方程组的解就是交点坐标;
④ 相交的条件是
相交的条件是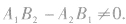
两点间的距离公式:
设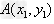 ,
, 是平面直角坐标系中的两个点,则
是平面直角坐标系中的两个点,则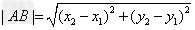 。
。
特别地,原点O(0,0)与任意一点P(x,y)的距离为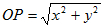
两点间的距离公式的理解:
(1)在公式中,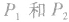 的位置是对称的,没有先后之分,即
的位置是对称的,没有先后之分,即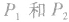 间的距离也可表示为
间的距离也可表示为
(2)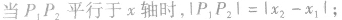

与“如图,直线 l1:y=kx+1-k(k≠0,k≠±)与l2:相交于点P,直线l...”考查相似的试题有:
- 已知数列{an}的首项为a1=3,an与前n项和Sn之间满足2an=Sn·Sn-1(n≥2),(1)求证:是等差数列,并求公差;(2)求数列{an}的通项...
- 已知偶函数f(x)=ax2+bx经过点(1,1),Sn为数列{an}的前n项和,点(n,Sn)(n∈N*)在曲线y=f(x)上。(1)求y=f(x)的解析式;...
- 设b>0,数列{an}满足a1=b,(n≥2)。(1)求数列{an}的通项公式;(2)证明:对于一切正整数n,2an≤bn+1+1。
- 直线过点和点,则直线的方程是( )A.B.C.D.
- 两条平行直线与之间的距离 .
- 直线3x+y–3=0与直线6x+my+1=0平行,则两直线之间的距离为___________。
- 已知直线l的倾斜角为135°,且经过点P(1,1),(Ⅰ)求直线l的方程;(Ⅱ)求点A(3,4)关于直线l的对称点A′的坐标。
- 已知直线l与3x+4y-7=0的倾斜角相等,并且与两坐标轴围成的三角形面积等于24,求直线l的方程.
- 已知直线l的方程为3x+4y-12=0,求直线l'的方程,使得:(1)l'与l平行,且过点(-1,3);(2)l'与l垂直,且l'与两轴围成的...
- 已知定点A(0,1),点B在直线x+y=0上运动,当线段AB最短时,点B的坐标是( )。