返回

高中数学

首页
首页 高中数学知识 等比数列的通项公式 数列的极限 用数量积表示两个向量的夹角 试题正文
  • 解答题
    已知一列非零向量
    an
    ，n∈N*，满足：
    a1
    =（10，-5），
    an
    =(xn，yn)=k(xn-1-yn-1，xn-1+yn-1)    ，（n32 ）．，其中k是非零常数．
    （1）求数列{|
    an
    |}是的通项公式；
    （2）求向量
    an-1
    与
    an
    的夹角；（n≥2）；
    （3）当k=
    1
    2
    时，把
    a1
    ，
    a2
    ，…，
    an
    ，…中所有与
    a1
    共线的向量按原来的顺序排成一列，记为
    b1
    ，
    b2
    ，…，
    bn
    ，…，令
    OBn
    =
    b1
    +
    b2
    +…+
    bn
    ，O为坐标原点，求点列{Bn}的极限点B的坐标．（注：若点坐标为（tn，sn），且
    lim
    n→∞
    tn=t    ，
    lim
    n→∞
    sn=s    ，则称点B（t，s）为点列的极限点．）
    本题信息：2007年杭州一模数学解答题难度较难 来源:未知
  • 本题答案
    查看答案
本试题 “已知一列非零向量an，n∈N*，满足：a1=（10，-5），an=(xn，yn)=k(xn-1-yn-1，xn-1+yn-1)，（n32 ）．，其中k是非零常数．（1）求数列{|an|}是的通项公式；（2...” 主要考查您对

等比数列的通项公式

数列的极限

用数量积表示两个向量的夹角

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 等比数列的通项公式
  • 数列的极限
  • 用数量积表示两个向量的夹角

等比数列的通项公式:

an=a1qn-1，q≠0，n∈N*。


等比数列的通项公式的理解：

①在已知a1和q的前提下，利用通项公式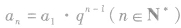可求出等比数列中的任意一项；
②在已知等比数列中任意两项的前提下，使用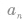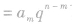可求等比数列中任何一项；
③用函数的观点看等比数列的通项，等比数列{an}的通项公式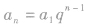，可以改写为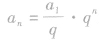．当q>o，且q≠1时，y=qx是一个指数函数，而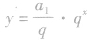是一个不为0的常数与指数函数的积，因此等比数列{an}的图象是函数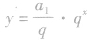的图象上的一群孤立的点；
④通项公式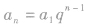亦可用以下方法推导出来：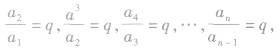

将以上（n一1）个等式相乘，便可得到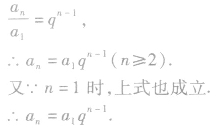
 
⑤用方程的观点看通项公式．在an，q，a1，n中，知三求一。


数列的极限定义（描述性的）：

如果当项数n无限增大时，无穷数列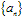的项an无限地趋近于某个常数a（即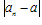无限地接近于0），a叫数列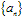的极限，记作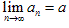，也可记做当n→+∞时，an→a。

数列的极限严格定义：

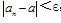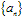即ε－N定义：对于任何正数ε（不论它多么小），总存在某正数N，使得当n＞N时，一切an都满足，a叫数列的极限。

数列极限的四则运算法则：

若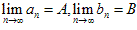，则
（1），；
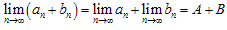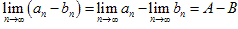（2），；
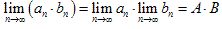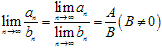（3）。
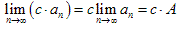前提条件：（1）各数列均有极限，（2）相加减时必须是有限个数列才能用法则。


an无限接近于a的方式有三种：

第一种是递增的数列，an无限接近于a，即an是在常数a的左边无限地趋近于a，如n→+∞时，；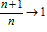
第二种是递减数列，an无限地趋近于a，即an是在常数a的右边无限地趋近于a，如n→+∞时，是；
第三种是摆动数列，an无限地趋近于a，即an是在无限摆动的过程中无限地趋近于a，如n→+∞时，。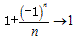


一些常用数列的极限：

（1）常数列A，A，A，…的极限是A；
（2）当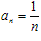时，；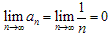
（3）当|q|＜1时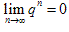，；当q＞1时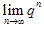，不存在；
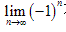（4）不存在，。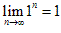
（5）无穷等比数列{an}中，首项a1，公比q，前n项和Sn，各项之和S，则（只有在0＜|q|＜1时）。


用数量积表示两个向量的夹角：

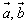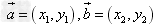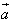设都是非零向量，，θ是与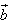的夹角，根据向量数量积的定义及坐标表示可得
。


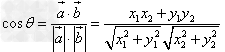向量数量积问题中方法提炼：

（1）平面向量的数量积的运算有两种形式，一是依据定义来计算，二是利用坐标来计算，具体应用哪种形式应根据已知条件的特征来选择；
（2）平面向量数量积的计算类似于多项式的运算，解题中要注意多项式运算方法的运用；
（3）平面向量数量积的计算中要注意平面向量基本定理的应用，选择合适的基底，以简化运算
（4）向量的数量积是一个数而不是一个向量。


发现相似题
与“已知一列非零向量an，n∈N*，满足：a1=（10，-5），an=(xn，yn...”考查相似的试题有：