本试题 “已知数列{an}满足:a1=,且an=(n≥2,n∈N*)。(1)求数列{an}的通项公式;(2)证明:对于一切正整数n,不等式a1·a2·…an<2·n!” 主要考查您对一般数列的通项公式
综合法与分析法证明不等式
数学归纳法证明不等式
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 一般数列的通项公式
- 综合法与分析法证明不等式
- 数学归纳法证明不等式
一般数列的定义:
如果数列{an}的第n项an与序号n之间的关系可以用一个式子表示成an=f(n),那么这个公式叫做这个数列的通项公式。
通项公式的求法:
(1)构造等比数列:凡是出现关于后项和前项的一次递推式都可以构造等比数列求通项公式;
(2)构造等差数列:递推式不能构造等比数列时,构造等差数列;
(3)递推:即按照后项和前项的对应规律,再往前项推写对应式。
已知递推公式求通项常见方法:
①已知a1=a,an+1=qan+b,求an时,利用待定系数法求解,其关键是确定待定系数λ,使an+1 +λ=q(an+λ)进而得到λ。
②已知a1=a,an=an-1+f(n)(n≥2),求an时,利用累加法求解,即an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)的方法。
③已知a1=a,an=f(n)an-1(n≥2),求an时,利用累乘法求解。
综合法:
利用某些已知的不等式或已证过的不等式或不等式的性质推导出所要证的不等式成立,这种证明方法叫综合法,即由因导果。利用均值不等式的有关公式最为常见。
分析法:
(1)从求证的不等式出发,分析使这个不等式成立的充分条件,把证明这个不等式的问题转化为这些条件是否具备的问题,如果能肯定这些条件都已具备,那么就可以判定所证的不等式成立,这种证明方法叫分析法,即执果索因;
(2)用分析法证明要注意格式:“若A成立,则B成立”的模式是:欲证B为真,只需证C为真,只需证D为真…最后得出A或已知的性质、公理、定理,从而得出B为真。也可使用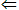 简化叙述。即B
简化叙述。即B C
C D
D …
… A或已知的性质、公理、定理。切不可使用B
A或已知的性质、公理、定理。切不可使用B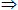 C
C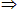 D
D …
…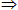 A。
A。
用综合法分析法证明不等式常用到的结论:

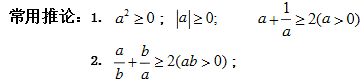
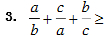 3,
3,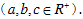
归纳法的定义:
由有限多个个别的特殊事例得出一般结论的推理方法,称为归纳法。
数学归纳法证明不等式的步骤:
(1)证明当n取初始值n0(例如n0=0,n0=1等)时不等式成立;
(2)假设当n=k(k为自然数,k≥n0)时不等式成立,证明当n=k+1时不等式也成立。
对数学归纳法的理解:
(1)数学归纳法是一种用于证明与自然数n有关的命题的正确性的证明方法.它的操作步骤简单、明确。
(2)运用数学归纳法证明与正整数有关的数学命题,两个步骤缺一不可.理解数学归纳法中的递推思想,尤其要注意其中第二步,证明n=k+1命题成立时必须要用到n=k时命题成立这个条件.这种理解不仅使我们能够正确认识数学归纳法的原理与本质,也为证明过程中第二步的设计指明了思维方向.
与“已知数列{an}满足:a1=,且an=(n≥2,n∈N*)。(1)求数列{an...”考查相似的试题有:
- 已知数列{an}满足:.(I)求数列{an}的通项公式;(II)设,求.
- 已知数列{an}满足:a1=2t,t2-2an-1t+an-1an=0,n=2,3,4,…(其中t为常数,且t≠0),(Ⅰ)求证:数列为等差数列;(Ⅱ)求数列{a...
- 某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少,从第2年到第6年,每年初M的价值比上年初减少10...
- 已知Sn为数列{an}的前n项和,,根据上述条件可归纳出这个数列的通项公式为an=( )。
- 设,求证:。
- 求证:若三棱锥的顶点到底面的射影是底面三角形的垂心,则底面三角形的任一顶点到所对侧面的射影也必是此三角形的垂心.
- 在中,不等式成立;在凸四边形ABCD中,不等式成立;在凸五边形ABCDE中,不等式成立,,依此类推,在凸n边形中,不等式__ ___...
- (本小题满分14分)一种计算装置,有一数据入口点A和一个运算出口点B ,按照某种运算程序:①当从A口输入自然数1时,从B口得到...
- 设数列的前项和为,且对任意都有:;(1)求;(2)猜想的表达式并证明.
- 是否存在a、b、c使得等式1·22+2·32+…+n(n+1)2=(an2+bn+c)