本试题 “在△ABC中,角A、B、C所对的边分别是a、b、c,且有bcosC=3acosB-ccosB(1)求cosB的值;(2)若·=2,b=2,求a和c的值。” 主要考查您对正弦定理
余弦定理
向量数量积的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 正弦定理
- 余弦定理
- 向量数量积的运算
正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即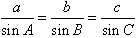 =2R。
=2R。
有以下一些变式:
(1)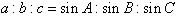 ;
;
(2)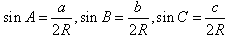 ;
;
(3)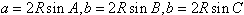 。
。
正弦定理在解三角形中的应用:
(1)已知两角和一边解三角形,只有一解。
(2)已知两边和其中一边的对角,解三角形,要注意对解的个数的讨论。可按如下步骤和方法进行:先看已知角的性质和已知两边的大小关系。
如已知a,b,A,
(一)若A为钝角或直角,当b≥a时,则无解;当a≥b时,有只有一个解;
(二)若A为锐角,结合下图理解。
①若a≥b或a=bsinA,则只有一个解。
②若bsinA<a<b,则有两解。
③若a<bsinA,则无解。 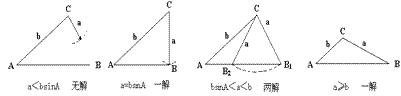
也可根据a,b的关系及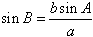 与1的大小关系来确定。
与1的大小关系来确定。
余弦定理:
三角形任意一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍,
即 。
。
推论:
在△ABC中,若a2+b2=c2,则C为直角;若a2+b2>c2,则C为锐角;若a2+b2<c2,则C为钝角。
余弦定理在解三角形中的应用:
(1)已知两边和夹角,
(2)已知三边。
其它公式:
射影公式: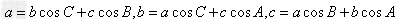
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量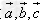 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)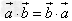 ;
;
(2)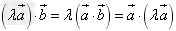 ;
;
(3)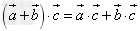 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“在△ABC中,角A、B、C所对的边分别是a、b、c,且有bcosC=3acos...”考查相似的试题有:
- 在△ABC中,a,b,c分别是BC,AC,AB三边的长,已知a=8,B=60°,C=75°,则b等于______.
- 已知△ABC满足:∠B=π3,AB=3,AC=7,则BC的长是( )A.2B.1C.1或2D.3
- 在△ABC中,B=45°,C=60°,c=1,则△ABC中最短边的边长等于( )A.12B.32C.62D.63
- 中,角、、的对边长分别为、、,已知,,,则_____________.
- 在△ABC中,内角A,B,C的对边边长分别是a,b,c,a2-b2-c2=bc,则A=______.
- 在中,角对边分别是,满足.(1)求角的大小;(2)求的最大值,并求取得最大值时角的大小.
- 在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足.(1)求角C的大小;(2)求sinA+sinB的最大值.
- 在△ABC中,C=60°,AB=3,AB边上的高为43,则AC+BC=______.
- 已知向量、,若=(2,1),=10,|-|=,则||=( ) A. B. C.5 D.25
- 下列命题正确的是( )A.若=,则=B.若|+|=|-|,则=0C.若//,//,则//D.若与是单位向量,则=1