本试题 “在平面直角坐标系xoy中,已知椭圆的左焦点,且在在上。(1)求的方程;(2)设直线l同时与椭圆和抛物线相切,求直线l的方程。” 主要考查您对直线的方程
椭圆的标准方程及图象
直线与椭圆方程的应用
直线与抛物线的应用
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 直线的方程
- 椭圆的标准方程及图象
- 直线与椭圆方程的应用
- 直线与抛物线的应用
直线方程的定义:
以一个方程的解为坐标的点都是某条直线上的点,这个方程就叫做这条直线的方程,这条直线叫做这个方程的直线。
基本的思想和方法:
求直线方程是解析几何常见的问题之一,恰当选择方程的形式是每一步,然后釆用待定系数法确定方程,在求直线方程时,要注意斜率是否存在,利用截距式时,不能忽视截距为0的情形,同时要区分“截距”和“距离”。
直线方程的几种形式:
1.点斜式方程:
(1)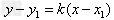 ,(直线l过点
,(直线l过点 ,且斜率为k)。
,且斜率为k)。
(2)当直线的斜率为0°时,k=0,直线的方程是y=y1。当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示,但因l上每一点的横坐标都等于x1,所以它的方程是x=x1。
2.斜截式方程:已知直线在y轴上的截距为b和斜率k,则直线的方程为:y=kx+b,它不包括垂直于x轴的直线。
3.两点式方程:已知直线经过(x1,y1),(x2,y2)两点,则直线方程为:
4.截距式方程:已知直线在x轴和y轴上的截距为a,b,则直线方程为: (a、b≠0)。
(a、b≠0)。
5.一般式方程:(1)定义:任何直线均可写成:Ax+By+C=0(A,B不同时为0)的形式。(2)特殊的方程如:平行于x轴的直线:y=b(b为常数);平行于y轴的直线:x=a(a为常数)。
几种特殊位置的直线方程:

(2)待定系数法:先设出直线的方程,再根据已知条件求出假设系数,最后代入直线方程,待定系数法常适用于斜截式,已知两点坐标等.
利用待定系数法求直线方程的步骤:①设方程;②求系数;③代入方程得直线方程,如果已知直线过一个定点
 ,可以利用直线的点斜式
,可以利用直线的点斜式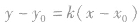 求方程,也可以利用斜截式、截距式等形式求解.
求方程,也可以利用斜截式、截距式等形式求解.椭圆的标准方程:
(1)中心在原点,焦点在x轴上: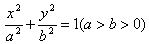 ;
;
(2)中心在原点,焦点在y轴上: 。
。
椭圆的图像:
(1)焦点在x轴: ;
;
(2)焦点在y轴: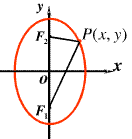 。
。
巧记椭圆标准方程的形式:
①椭圆标准方程的形式:左边是两个分式的平方和,右边是1;
②椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在哪一个轴上;
③椭圆的标准方程中,三个参数a,b,c满足a2= b2+ c2;
④由椭圆的标准方程可以求出三个参数a,b,c的值.
待定系数法求椭圆的标准方程:
求椭圆的标准方程常用待定系数法,要恰当地选择方程的形式,如果不能确定焦点的位置,那么有两种方法来解决问题:一是分类讨论,全面考虑问题;二是可把椭圆的方程设为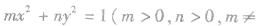 n)用待定系数法求出m,n的值,从而求出标准方程,
n)用待定系数法求出m,n的值,从而求出标准方程,
直线与椭圆的方程:
设直线l的方程为:Ax+By+C=0(A、B不同时为零),椭圆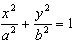 (a>b>0),将直线的方程代入椭圆的方程,消去y(或x)得到一元二次方程,进而应用根与系数的关系解题。
(a>b>0),将直线的方程代入椭圆的方程,消去y(或x)得到一元二次方程,进而应用根与系数的关系解题。
椭圆的焦半径、焦点弦和通径:
(1)焦半径公式:
①焦点在x轴上时:|PF1|=a+ex0,|PF2|=a-ex0;
②焦点在y轴上时:|PF1|=a+ey0,|PF2|=a-ey0;
(2)焦点弦:
过椭圆焦点的弦称为椭圆的焦点弦.设过椭圆 的弦为AB,其中A(x1,y1),B(x2,y2),则|AB|=2a+e(x1+x2).由此可见,过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数.
的弦为AB,其中A(x1,y1),B(x2,y2),则|AB|=2a+e(x1+x2).由此可见,过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数.
(3)通径:过椭圆的焦点与椭圆的长轴垂直的直线被椭圆所截得的线段称为椭圆的通径,其长为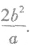
椭圆中焦点三角形的解法:
椭圆上的点与两个焦点F1,F2所构成的三角形,通常称之为焦点三角形,解焦点三角形问题经常使用三角形边角关系定理,解题中,通过变形,使之出现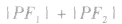 ,这样便于运用椭圆的定义,得到a,c的关系,打开解题思路,整体代换求
,这样便于运用椭圆的定义,得到a,c的关系,打开解题思路,整体代换求 是这类问题中的常用技巧。
是这类问题中的常用技巧。
关于椭圆的几个重要结论:
(1)弦长公式: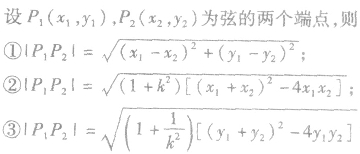
(2)焦点三角形: 上异于长轴端点的点,
上异于长轴端点的点,
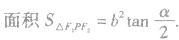
(3)以椭圆的焦半径为直径的圆必与以长轴为直径的圆内切.
(4)椭圆的切线: 处的切线方程为
处的切线方程为
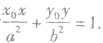
(5)对于椭圆
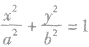 ,我们有
,我们有

设直线l的方程为:Ax+By+C=0(A、B不同时为零),抛物线的方程为y2=2px(p>0),将直线的方程代入抛物线的方程,消去y(或x) 得到一元二次方程,进而应用根与系数的关系解题。
直线与抛物线的位置关系:
直线和抛物线的位置关系,可通过直线方程与抛物线方程组成的方程组的实数解的个数来确定,同时注意过焦点的弦的一些性质,如:
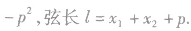
与“在平面直角坐标系xoy中,已知椭圆的左焦点,且在在上。(1)...”考查相似的试题有:
- 过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是[ ]A.4x-3y-19=0B.4x+3y-13=0C.3x-4y-16=0D.3x+4y-8=0
- 已知直线l过点(0,-1),且与直线y=-x+2垂直,则直线l的方程为( )A.y=x-1B.y=x+1C.y=-x-1D.y=-x+1
- 已知椭圆的左,右两个顶点分别为A、B,曲线C是以A、B两点为顶点,焦距为的双曲线。设点P在第一象限且在曲线C上,直线AP与椭圆...
- 设直线l的方程为(a+1)x+y-2-a=0(x∈R).(1)若直线l在两坐标轴上的截距相等,求直线l的方程;(2)若a>-1,直线l与x轴、...
- 如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求:(Ⅰ)AB边上的中线CM所在直线的一般方程;(Ⅱ)求△ABC的面...
- 直线绕坐标原点逆时针方向旋转30°后所得直线被圆截得的弦长为( )A.B.2C.D.
- 已知在平面直角坐标系xoy中,向量,△OFP的面积为,且.(I)设4求向量与的夹角的取值范围;(II)设以原点O为中心,对称轴在坐...
- 过椭圆C:x26+y22=1的右焦点F作斜率为k(k>0)的直线l与椭圆交于A、B两点,且坐标原点O到直线l的距离d满足:0<d<233.(I)...
- 已知椭圆,过右焦点F作不垂直于x轴的弦交椭圆于B两点,AB的垂直平分线交x轴于N,则|NF|:|AB|等于( ) A. B. C. D.
- 已知曲线C上任意一点M到点F(0,1)的距离比它到直线l:y=﹣2的距离小1.(1)求曲线C的方程;(2)过点P(2,2)的直线与曲...