本试题 “已知向量a=(x,y),b=(cosα,sinα),其中x,y,α∈R,若|a|=4|b|,则a•b<λ2成立的一个必要而不充分条件是( )A.-3<λ<3B.-1<λ<1C.λ>3或λ<-3D.λ...” 主要考查您对充分条件与必要条件
向量数量积的运算
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 充分条件与必要条件
- 向量数量积的运算
1、充分条件与必要条件:一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可推出q,记作 ,并且说p是q的充分条件,q是p的必要条件;
,并且说p是q的充分条件,q是p的必要条件;
2、充要条件:一般地,如果既有 ,又有
,又有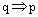 ,就记作
,就记作 ,此时,我们说,p是q的充分必要条件,简称充要条件。
,此时,我们说,p是q的充分必要条件,简称充要条件。
概括的说,如果 ,那么p与q互为充要条件。
,那么p与q互为充要条件。
3、充分不必要条件、必要不充分条件、既不充分也不必要条件:
①充分不必要条件:如果 ,且p
,且p q,则说p是q的充分不必要条件;
q,则说p是q的充分不必要条件;
②必要不充分条件:如果p q,且
q,且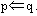 ,则说p是q的必要不充分条件;
,则说p是q的必要不充分条件;
③既不充分也不必要条件:如果p q,且p
q,且p q,则说p是q的既不充分也不必要条件。
q,则说p是q的既不充分也不必要条件。
两个向量数量积的含义:
如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为 ,我们把数量
,我们把数量 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作: ,即
,即 。
。 叫
叫 在
在 上的投影。
上的投影。
规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。
数量积的的运算律:
已知向量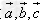 和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
和实数λ,下面(1)(2)(3)分别叫做交换律,数乘结合律,分配律。
(1)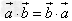 ;
;
(2)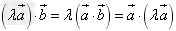 ;
;
(3)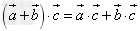 。
。
向量数量积的性质:
设两个非零向量
(1) ;
;
(2) ;
;
(3) ;
;
(4) ;
;
(5)当 ,
, 同向时,
同向时, ;当
;当 与
与 反向时,
反向时, ;当
;当 为锐角时,
为锐角时, 为正且
为正且 ,
, 不同向,
不同向, ;当
;当 为钝角时,
为钝角时, 为负且
为负且 ,
, 不反向,
不反向, 。
。
发现相似题
与“已知向量a=(x,y),b=(cosα,sinα),其中x,y,α∈R,若|a...”考查相似的试题有:
- 已知p 是r 的充分条件而不是必要条件,s 是r的必要条件,q是r的充分条件,q是s的必要条件,现有下列命题:①s 是q 的充要条件...
- 已知函数f(x)=4sinxcosx-23cos2x+1,且给定条件p:“π4≤x≤π2”.(1)求f(x)在给定条件p下的最大值及最小值;(2)若又给条件...
- 甲:A1、A2是互斥事件;乙:A1、A2是对立事件,那么( )A.甲是乙的充分但不必要条件B.甲是乙的必要但不充分条件C.甲是乙...
- 求证:方程x2+ax+1=0的两实根的平方和大于3的必要条件是|a|>,这个条件是其充分条件吗?为什么?
- 下列说法正确的是______.①“x=1”是“|x|=1”的充分不必要条件;②若命题p:∃b∈R,使f(x)=x2+bx+1是偶函数,则¬p:∀b∈R,f(x)...
- 下列有关命题的说法正确的是[ ]A.命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”B.命题“若x=y,则sinx=siny”的逆否命题为真...
- 设a=(sinx,3cosx),b=(sinx+2cosx,cosx),c=(0,-1),(1)记f(x)=a•b,求f(x)的最小正周期;(2)把f(x)的图...
- 在平面直角坐标系xOy中,点A(﹣1,﹣2)、B(2,3)、C(﹣2,﹣1).(1)求以线段AB、AC为邻边的平行四边形两条对角线的长...
- 过点M(2,0)作圆x2+y2=1的两条切线MA,MB(A,B为切点),则MA•MB=( )A.532B.52C.332D.32
- 已知F1,F2是椭圆x2a2+y2b2=1(a>b>0)的两个焦点,O为坐标原点,点P(-1,22)在椭圆上,且PF1•F1F2=0,⊙O是以F1F2为直径...