本试题 “在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列,(1)求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并...” 主要考查您对等差中项
等比中项
一般数列的通项公式
反证法与放缩法
数学归纳法
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 等差中项
- 等比中项
- 一般数列的通项公式
- 反证法与放缩法
- 数学归纳法
等差中项:
若a,A,b成等差数列,那么A叫做a与b的等差中项,且2A=a+b,即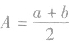 ,反之,若
,反之,若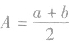 ,则a,A,b成等差数列。
,则a,A,b成等差数列。
等差数列中相邻三项之间存在如下关系:
(1)
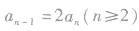 反之,若数列中相邻三项之间存在如下关系:
反之,若数列中相邻三项之间存在如下关系: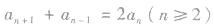 则该数列是等差数列,
则该数列是等差数列,
(2) 若a,A,b成等差数列,那么 2A=a+b,A-a =b -A,a-A =A -b都是等价的.
2A=a+b,A-a =b -A,a-A =A -b都是等价的.
等比中项:
若数a,G,b成等比数列,那么就称G为a与b的等比中项,从而有G2=ab或G=±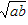 。
。
等比中项的理解:
如果a,G,b三个数成等比数列,则有G2=ab.反之不一定成立.由等比中项定义可知: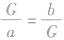 ,
, 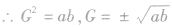 ,
,
这表明,只有同号的两项才有等比中项,并且这两项有2个互为相反数的等比中项,当a>0,b>0时,G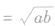 又叫做a,b的几何平均数。
又叫做a,b的几何平均数。
一般数列的定义:
如果数列{an}的第n项an与序号n之间的关系可以用一个式子表示成an=f(n),那么这个公式叫做这个数列的通项公式。
通项公式的求法:
(1)构造等比数列:凡是出现关于后项和前项的一次递推式都可以构造等比数列求通项公式;
(2)构造等差数列:递推式不能构造等比数列时,构造等差数列;
(3)递推:即按照后项和前项的对应规律,再往前项推写对应式。
已知递推公式求通项常见方法:
①已知a1=a,an+1=qan+b,求an时,利用待定系数法求解,其关键是确定待定系数λ,使an+1 +λ=q(an+λ)进而得到λ。
②已知a1=a,an=an-1+f(n)(n≥2),求an时,利用累加法求解,即an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)的方法。
③已知a1=a,an=f(n)an-1(n≥2),求an时,利用累乘法求解。
反证法的定义:
有些不等式无法利用题设的已知条件直接证明,我们可以用间接的方法——反证法去证明,即通过否定原结论——导出矛盾——从而达到肯定原结论的目的。
放缩法的定义:
把原不等式放大或缩小成一个恰好可以化简的形式,比较常用的方法是把分母或分子适当放大或缩小(减去或加上一个正数)使不等式简化易证。
反证法证题的步骤:
若A成立,求证B成立。
共分三步:
(1)提出与结论相反的假设;如负数的反面是非负数,正数的反面是非正数即0和负数;
(2)从假设出发,经过推理,得出矛盾;(必须由假设出发进行推理否则不是反证法或证错);
(3)由矛盾判定假设不正确,从而肯定命题的结论正确.矛盾:与定义、公理、定理、公式、性质等一切已有的结论矛盾甚至自相矛盾。
反证法是一种间接证明命题的基本方法。在证明一个数学命题时,如果运用直接证明法比较困难或难以证明时,可运用反证法进行证明。
放缩法的意义:
放缩法理论依据是不等式的传递性:若,a<b,b<c,则a<c.
放缩法的操作:
若求证P<Q,先证P<P1<P2<…<Pn,再证恰有Pn<Q.
需注意:(1)只有同方向才可以放缩,反方向不可。
(2)不能放(缩)得太大(小),否则不会有最后的Pn<Q.
归纳法:
对于某类事物,由它的一些特殊事例或其全部可能情况,归纳出一般结论的推理方法叫做归纳法。归纳法包括完全归纳法和不完全归纳法。
数学归纳法:
一般地,证明一个与正整数n有关的命题,可按下列步骤进行:
(1)证明当n取第一个值n0(n0∈N*)时命题成立;
(2)假设当n=k(k∈N*,k≥n0)时命题成立,证明当n=k+1时命题也成立;
完成这两步,就可以断定这个命题对从n0开始的所有正整数n都成立,这种证明方法叫做数学归纳法。
数学归纳法的特点:
①用数学归纳法进行证明时,要分两个步骤,两步同样重要,两步骤缺一不可;
②第二步证明,由假设n=k时命题成立,到n=k+1时.必须用假设条件,否则不是数学归纳法;
③最后一定要写“由(1)(2)……”。
数学归纳法的应用:
(1)证明恒等式;
(2)证明不等式;
(3)三角函数;
(4)计算、猜想、证明。
与“在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列...”考查相似的试题有:
- 已知数列是各项均为正数的等差数列,且公差不为0,则以下各式中一定正确的为( )A.a1a84a5B.a1a8>a4a5C.a1+a8>a4+a5D.a1...
- 设{an}是公差不为0的等差数列,a1=2且a1,a3,a6成等比数列,则{an}的前n项和Sn=A.B.C.D.n2+n
- 已知a,b,c为正实数,a+b+c=1. 求证:(1)a2+b2+c2≥(2)≤6
- 已知函数(a,b,c为常数,a≠0)。(1)若c=0时,数列{an}满足条件:点(n,an)在函数的图象上,求{an}的前n项和Sn;(2)在...
- (几何证明选讲选做题)如右图,从圆外一点引圆的切线和割线,已知,,圆的半径为3,则圆心到直线的距离为 .
- 已知函数的图象经过其中e为自然对数的底数,e≈2.71,(Ⅰ)求实数a;(Ⅱ)求f(x)的单调区间;(Ⅲ)证明:对于任意的n∈N*,都...
- 用反证法证明命题“如果a>b,那么”时,假设的内容是( ) A. B. C.或 D.或
- 已知函数f(x)=ln(1+x)-x,g(x)=xlnx,(1)求函数f(x)的最大值;(2)设0<a<b,证明:0<g(a)+g(b)-2g()<(b-a)ln2。
- 已知数列{an}的前n项和为Sn,且对任意正整数n都有2Sn=(n+2)an-1.(Ⅰ)求数列{an}的通项公式;(Ⅱ)设Tn=1a1•a3+1a2•a4+…+1...
- 用数学归纳法证明12+cosα+cos3α+…+cos(2n-1)α=sin2n+12a•cos2n-12asina(k∈Z*,α≠kπ,n∈N+),在验证n=1时,左边计算所得的...