等比数列的通项公式:

a_n=a₁q^n-1，q≠0，n∈N^*。

等比数列的通项公式的理解：

①在已知a₁和q的前提下，利用通项公式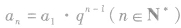可求出等比数列中的任意一项；
②在已知等比数列中任意两项的前提下，使用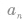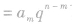可求等比数列中任何一项；
③用函数的观点看等比数列的通项，等比数列{a_n}的通项公式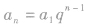，可以改写为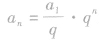．当q>o，且q≠1时，y=q^x是一个指数函数，而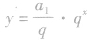是一个不为0的常数与指数函数的积，因此等比数列{a_n}的图象是函数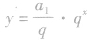的图象上的一群孤立的点；
④通项公式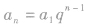亦可用以下方法推导出来：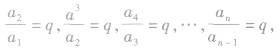

将以上（n一1）个等式相乘，便可得到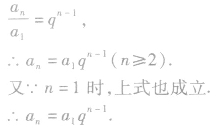
 
⑤用方程的观点看通项公式．在a_n，q，a₁，n中，知三求一。

等比数列的前n项和公式：

；

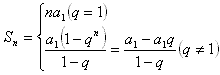等比数列中设元技巧：

已知a₁，q，n，a_n ，S_n中的三个量，求其它两个量，是归结为解方程组问题，知三求二。
注意设元的技巧，如奇数个成等比数列，可设为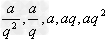：…，…（公比为q），但偶数个数成等比数列时，不能设为…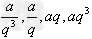，…因公比不一定为一个正数，公比为正时可如此设。

等比数列前n项和公式的变形：
q≠1时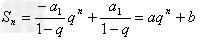，（a≠0，b≠0，a+b=0）；

等比数列前n项和常见结论：
一个等比数列有3n项，若前n项之和为S₁，中间n项之和为S₂，最后n项之和为S₃，当q≠-1时，S₁，S₂，S₃为等比数列。

数列求和的常用方法：

1.裂项相加法：数列中的项形如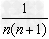的形式，可以把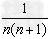表示为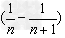，累加时抵消中间的许多项，从而求得数列的和；
2、错位相减法：源于等比数列前n项和公式的推导，对于形如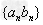的数列，其中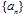为等差数列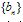，为等比数列，均可用此法；
3、倒序相加法：此方法源于等差数列前n项和公式的推导，目的在于利用与首末两项等距离的两项相加有公因式可提取，以便化简后求和。
4、分组转化法：把数列的每一项分成两项，或把数列的项“集”在一块重新组合，或把整个数列分成两个部分，使其转化为等差或等比数列，这一求和方法称为分组转化法。
5、公式法求和：所给数列的通项是关于n的多项式，此时求和可采用公式求和，常用的公式有：
 
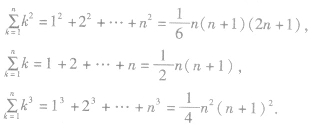
数列求和的方法多种多样，要视具体情形选用合适方法。

数列求和特别提醒：

（1）对通项公式含有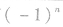的一类数列，在求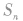时，要注意讨论n的奇偶性；
（2）在用等比数列前n项和公式时，一定要分q=1和q≠1两种情况来讨论。

比较法分类：

（1）求差比较法：要证a＞b，只要证a-b＞0；
（2）求商比较法：要证a＞b，且b＞0，只要证＞1；

比较法的步骤是：

作差（商）后通过分解因式、配方、通分等手段变形判断符号或与1的大小，然后作出结论。

实数比较大小的依据：

在数轴上不同的点A与点B分别表示两个不同的实数a与b，右边的点表示的数比左边的点表示的数大，从实数减法在数轴上的表示可以看出a、b之间具有以下性质：如图，如果a-b是正数，那么a>b;如果a-b是负数，那么a<b;如果a-b等于零，那么a=b，反之也成立，从而a-b>0等价于a>b;a-b=0等价于a=b;a-b<0等价于a<b． 

比较数（式）的大小常用的方法：

（1）一是利用作差法来判断差的符号；二是利用作商法（分母为正时）来判断商与1的大小。这两种方法的关键是变形，常用的变形的技巧有因式分解、通分、配方、有理化等，当两个代数式正负不确定且为多项式形式时常用作差法比较大小．当两个代数式均为正且为幂的乘积式时常用作商法比较大小．
(2)比较大小时应熟记并应用“若a>b且ab>0则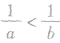”这一结论，不能强化也不能弱化条件，在此时应引起特别重视。