二次函数的定义：

一般地，如果（a，b，c是常数，a≠0），那么y叫做x的二次函数。

二次函数的图像：

是一条关于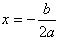对称的曲线，这条曲线叫抛物线。
抛物线的主要特征：①有开口方向，a表示开口方向；a＞0时，抛物线开口向上；a<0时，抛物线开口向下；
②有对称轴；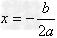
③有顶点；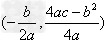
④c表示抛物线与y轴的交点坐标：（0，c）。

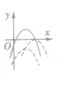
性质：二次函数y=ax²+bx+c，

①当a＞0时，函数f（x）的图象开口向上，在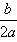（-∞，-）上是减函数，在[-，＋∞）上是增函数；
②当a<0时，函数f（x）的图象开口向下，在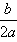（-∞，-）上是增函数，在[-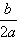，＋∞）是减函数。

二次函数（a，b，c是常数，a≠0）的图像：

图像	函数的性质
a>0	定义域	x∈R(个别题目有限制的，由解析式确定)
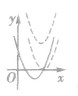	值域	a>0	a<0
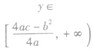	奇偶性	b=0时为偶函数，b≠0时为非奇非偶函数
a<0	单调性	a>0	a<0
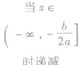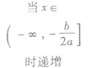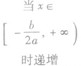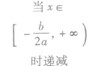	图像特点

二次函数的解析式：

（1）一般式：（a，b，c是常数，a≠0）；
（2）顶点式：若二次函数的顶点坐标为（h,k），则其解析式为 ;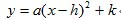
（3）双根式：若相应一元二次方程的两个根为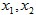 ,则其解析式为 。

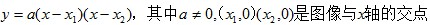二次函数在闭区间上的最值的求法：

(1)二次函数 在区间[p,g]上的最值问题
一般情况下，需要分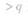三种情况讨论解决．
当a>0时，f(x)在区间[p，g]上的最大值为M，最小值为m，令 ．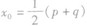
①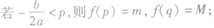 
②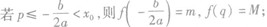
③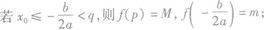
④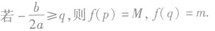
特别提醒：在区间内同时讨论最大值和最小值需要分四种情况讨论．

(2)二次函数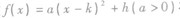在区间[m．n]上的最值问题一般地，有以下结论：
 
特别提醒：max{1,2}=2,即取集合{1,2}中最大的元素。

二次函数的应用：

（1）应用二次函数才解决实际问题的一般思路：
理解题意；建立数学模型；解决题目提出的问题。
（2）应用二次函数求实际问题中的最值：
即解二次函数最值应用题，设法把关于最值的实际问题转化为二次函数的最值问题，然后按求二次函数最值的方法求解。求最值时，要注意求得答案要符合实际问题。

线面平行的定义：

若直线和平面无公共点，则称直线和平面平行。

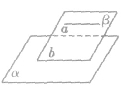
线面平行的判定定理：

平面外一条直线与此平面内一条直线平行，则该直线与此平面平行。 线线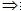平行线面平行

符号语言：

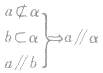
 线面平行的性质定理：

如果一条直线和一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行。 线面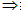平行线线平行

 符号语言：

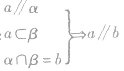
证明直线与平面平行的常用方法：

(l)反证法，即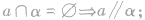 
(2)判定定理法，即 
(3)面面平行的性质定理，即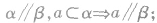 
(4)向量法，平面外的直线的方向向量n与平面的法向量n垂直，则直线与平面平行，即

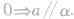
直线方程的定义：

以一个方程的解为坐标的点都是某条直线上的点，这个方程就叫做这条直线的方程，这条直线叫做这个方程的直线。

基本的思想和方法：

求直线方程是解析几何常见的问题之一，恰当选择方程的形式是每一步，然后釆用待定系数法确定方程，在求直线方程时，要注意斜率是否存在，利用截距式时，不能忽视截距为0的情形，同时要区分“截距”和“距离”。

直线方程的几种形式：

1.点斜式方程：
（1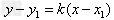），（直线l过点，且斜率为k）。
（2）当直线的斜率为0°时，k=0，直线的方程是y=y₁。当直线的斜率为90°时，直线的斜率不存在，它的方程不能用点斜式表示，但因l上每一点的横坐标都等于x₁，所以它的方程是x=x₁。
2.斜截式方程：已知直线在y轴上的截距为b和斜率k，则直线的方程为：y=kx+b，它不包括垂直于x轴的直线。
3.两点式方程：已知直线经过（x₁，y₁），（x₂，y₂）两点，则直线方程为：
4.截距式方程：已知直线在x轴和y轴上的截距为a，b，则直线方程为：（a、b≠0）。
5.一般式方程：（1）定义：任何直线均可写成：Ax+By+C=0（A，B不同时为0）的形式。（2）特殊的方程如：平行于x轴的直线：y=b（b为常数）；平行于y轴的直线：x=a（a为常数）。

几种特殊位置的直线方程：

(1)直接法：根据已知条件，选择适当的直线方程形式，直接求出直线方程．应明确直线方程的几种形式及各自的特点，合理选择解决方法，一般地，已知一点通常选择点斜式；已知斜率选择斜截式或点斜式；已知在两坐标轴上的截距用截距式；已知两点用两点式，这时应特别注意斜率不存在的情况．
(2)待定系数法：先设出直线的方程，再根据已知条件求出假设系数，最后代入直线方程，待定系数法常适用于斜截式，已知两点坐标等．
利用待定系数法求直线方程的步骤：①设方程；②求系数；③代入方程得直线方程，如果已知直线过一个定点,可以利用直线的点斜式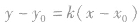求方程，也可以利用斜截式、截距式等形式求解．