本试题 “已知函数f(x)=x3+bx2+cx的导函数的图象关于直线x=2对称。(1)求b的值;(2)若f(x)在x=t处取得极小值,记此极小值为g(t),求g(t)的定义域和值域。” 主要考查您对函数的定义域、值域
二次函数的性质及应用
导数的运算
函数的极值与导数的关系
等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
- 函数的定义域、值域
- 二次函数的性质及应用
- 导数的运算
- 函数的极值与导数的关系
定义域、值域的概念:
自变量取值范围叫做函数的定义域,函数值的集合叫做函数的值域。
1、求函数定义域的常用方法有:
(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零等;
(2)根据实际问题的要求确定自变量的范围;
(3)根据相关解析式的定义域来确定所求函数自变量的范围;
(4)复合函数的定义域:如果y是u的函数,而u是x的函数,即y=f(u),u=g(x),那么y=f[g(x)]叫做函数f与g的复合函数,u叫做中间变量,设f(x)的定义域是x∈M,g(x)的定义域是x∈N,求y=f[g(x)]的定义域时,则只需求满足 的x的集合。设y=f[g(x)]的定义域为P,则
的x的集合。设y=f[g(x)]的定义域为P,则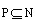 。
。
3、求函数值域的方法:
(1)利用一些常见函数的单调性和值域,如一次函数,二次函数,反比例函数,指数函数,对数函数,三角函数,形如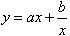 (a,b为非零常数)的函数;
(a,b为非零常数)的函数;
(2)利用函数的图象即数形结合的方法;
(3)利用均值不等式;
(4)利用判别式;
(5)利用换元法(如三角换元);
(6)分离法:分离常数与分离参数两种形式;
(7)利用复合函数的单调性。(注:二次函数在闭区间上的值域要特别注意对称轴与闭区间的位置关系,含字母时要注意讨论)
二次函数的定义:
一般地,如果 (a,b,c是常数,a≠0),那么y叫做x的二次函数。
(a,b,c是常数,a≠0),那么y叫做x的二次函数。
二次函数的图像:
是一条关于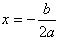 对称的曲线,这条曲线叫抛物线。
对称的曲线,这条曲线叫抛物线。
抛物线的主要特征:①有开口方向,a表示开口方向;a>0时,抛物线开口向上;a<0时,抛物线开口向下;
②有对称轴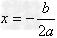 ;
;
③有顶点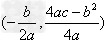 ;
;
④c表示抛物线与y轴的交点坐标:(0,c)。
性质:二次函数y=ax2+bx+c,
①当a>0时,函数f(x)的图象开口向上,在(-∞,-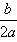 )上是减函数,在[-
)上是减函数,在[- ,+∞)上是增函数;
,+∞)上是增函数;
②当a<0时,函数f(x)的图象开口向下,在(-∞,-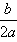 )上是增函数,在[-
)上是增函数,在[-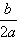 ,+∞)是减函数。
,+∞)是减函数。
二次函数 (a,b,c是常数,a≠0)的图像:
(a,b,c是常数,a≠0)的图像:
| 图像 | 函数的性质 | ||
| a>0 | 定义域 | x∈R(个别题目有限制的,由解析式确定) | |
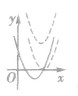 |
值域 | a>0 | a<0 |
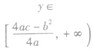 |
 | ||
| 奇偶性 | b=0时为偶函数,b≠0时为非奇非偶函数 | ||
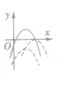
| a<0 | 单调性 | a>0 | a<0 |
 |
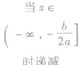 |
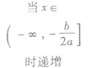 | |
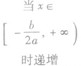 |
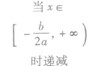 | ||
| 图像特点 |
 | ||
二次函数的解析式:
(1)一般式: (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);
(2)顶点式:若二次函数的顶点坐标为(h,k),则其解析式为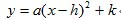 ;
;
(3)双根式:若相应一元二次方程的两个根为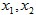 ,则其解析式为
,则其解析式为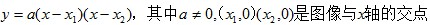 。
。
二次函数在闭区间上的最值的求法:
(1)二次函数![]() 在区间[p,g]上的最值问题
在区间[p,g]上的最值问题
一般情况下,需要分![]()
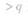 三种情况讨论解决.
三种情况讨论解决.
当a>0时,f(x)在区间[p,g]上的最大值为M,最小值为m,令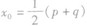 .
.
①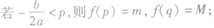
②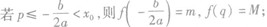
③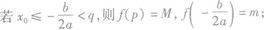
④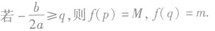
特别提醒:在区间内同时讨论最大值和最小值需要分四种情况讨论.
(2)二次函数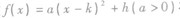 在区间[m.n]上的最值问题一般地,有以下结论:
在区间[m.n]上的最值问题一般地,有以下结论:
特别提醒:max{1,2}=2,即取集合{1,2}中最大的元素。
二次函数的应用:
(1)应用二次函数才解决实际问题的一般思路:
理解题意;建立数学模型;解决题目提出的问题。
(2)应用二次函数求实际问题中的最值:
即解二次函数最值应用题,设法把关于最值的实际问题转化为二次函数的最值问题,然后按求二次函数最值的方法求解。求最值时,要注意求得答案要符合实际问题。
常见函数的导数:
(1)C′=0 ;(2)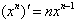 ;(3)
;(3)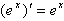 ;(4)
;(4) ;(5)
;(5)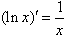 ;(6)
;(6)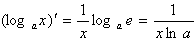 ;(7)
;(7)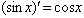 ;(8)
;(8)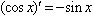
导数的四则运算:
(1)和差: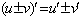
(2)积: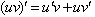
(3)商:
复合函数的导数:
运算法则复合函数导数的运算法则为: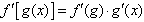
复合函数的求导的方法和步骤:
(1)分清复合函数的复合关系,选好中间变量;
(2)运用复合函数求导法则求复合函数的导数,注意分清每次是哪个变量对哪个变量求导数;
(3)根据基本函数的导数公式及导数的运算法则求出各函数的导数,并把中间变量换成自变量的函数。
求复合函数的导数一定要抓住“中间变量”这一关键环节,然后应用法则,由外向里一层层求导,注意不要漏层。
极值的定义:
(1)极大值: 一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)<f(x0),就说f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0),x0是极大值点;
(2)极小值:一般地,设函数f(x)在x0附近有定义,如果对x0附近的所有的点,都有f(x)>f(x0),就说f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0),x0是极小值点。
极值的性质:
(1)极值是一个局部概念,由定义知道,极值只是某个点的函数值与它附近点的函数值比较是最大或最小,并不意味着它在函数的整个的定义域内最大或最小;
(2)函数的极值不是唯一的,即一个函数在某区间上或定义域内极大值或极小值可以不止一个;
(3)极大值与极小值之间无确定的大小关系,即一个函数的极大值未必大于极小值;
(4)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点,而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点。
判别f(x0)是极大、极小值的方法:
若x0满足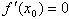 ,且在x0的两侧f(x)的导数异号,则x0是f(x)的极值点,
,且在x0的两侧f(x)的导数异号,则x0是f(x)的极值点, 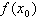 是极值,并且如果
是极值,并且如果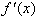 在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果
在x0两侧满足“左正右负”,则x0是f(x)的极大值点,f(x0)是极大值;如果 在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值。
在x0两侧满足“左负右正”,则x0是f(x)的极小值点,f(x0)是极小值。
求函数f(x)的极值的步骤:
(1)确定函数的定义区间,求导数f′(x);
(2)求方程f′(x)=0的根;
(3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格,检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号即都为正或都为负,则f(x)在这个根处无极值。
对函数极值概念的理解:
极值是一个新的概念,它是研究函数在某一很小区域时给出的一个概念,在理解极值概念时要注意以下几点:
①按定义,极值点x0是区间[a,b]内部的点,不会是端点a,b(因为在端点不可导).如图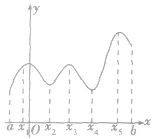
②极值是一个局部性概念,只要在一个小领域内成立即可.要注意极值必须在区间内的连续点取得.一个函数在定义域内可以有许多个极小值和极大值,在某一点的极小值也可能大于另一个点的极大值,也就是说极大值与极小值没有必然的大小关系,即极大值不一定比极小值大,极小值不一定比极大值小,如图.
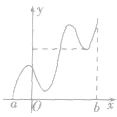
③若fx)在(a,b)内有极值,那么f(x)在(a,b)内绝不是单调函数,即在区间上单调的函数没有极值.
④若函数f(x)在[a,b]上有极值且连续,则它的极值点的分布是有规律的,相邻两个极大值点之间必有一个极小值点,同样相邻两个极小值点之间必有一个极大值点,一般地,当函数f(x)在[a,b]上连续且有有
限个极值点时,函数f(x)在[a,b]内的极大值点、极小值点是交替出现的,
⑤可导函数的极值点必须是导数为0的点,但导数为0的点不一定是极值点,不可导的点也可能是极值点,也可能不是极值点,
与“已知函数f(x)=x3+bx2+cx的导函数的图象关于直线x=2对称。(...”考查相似的试题有:
- 函数f(x)=|x2-a|在区间[-1,1]上的最大值M(a)的最小值是( )A.14B.12C.1D.2
- 函数,(1)若的定义域为R,求实数的取值范围.(2)若的定义域为[-2,1],求实数的值
- 设全集U=R,函数y=log2(6-x-x2)的定义域为A,函数y=1x2-x-12的定义域为B (1)求集合A与B;(2)求A∩B、(CUA)∪B
- .函数=的定义域为( )A.[1,+∞)B.[,1]C.(,+∞)D.(,1]
- 函数y=f(x)的定义域为[-1,1],值域为[0,1]则f(x-2)的定义域和值域为( )A.[1,3],[0,1]B.[-1,1],[0,1]C.[-1,...
- 如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝。再用S平方米塑料片制成圆柱的侧面和下底...
- 已知函数f(x)=ax2-2ax+2+b(a≠0),若f(x)在区间[2,3]上有最大值5,最小值2,(1)求a,b的值;(2)若b<1,g(x)=f(x)-mx在[2,4]...
- 已知0<x<1,则x(1-x)的最大值为______.
- 若f(x)=x(x+1)(x+2)…..(x+n),则
- 求下列函数的导数:;