返回

高中三年级数学

首页
首页 高中三年级数学知识 导数的概念及其几何意义 等比数列的定义及性质 一般数列的通项公式 等比数列的前n项和 反证法与放缩法 试题正文
  • 解答题
    已知函数f（x）=x2-4，设曲线y=f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1，0）（n∈N*），其中x1为正实数。
    （1）用xn表示xn+1；
    （2）若x1=4，记，证明数列{an}成等比数列，并求数列{xn}的通项公式；
    （3）若x1=4，bn=xn-2，Tn是数列{bn}的前n项和，证明Tn＜3。
    本题信息：2007年四川省高考真题数学解答题难度极难 来源:刘佩
  • 本题答案
    查看答案
本试题 “已知函数f（x）=x2-4，设曲线y=f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1，0）（n∈N*），其中x1为正实数。（1）用xn表示xn+1；（2）若x1=4，记...” 主要考查您对

导数的概念及其几何意义

等比数列的定义及性质

一般数列的通项公式

等比数列的前n项和

反证法与放缩法

等考点的理解。关于这些考点您可以点击下面的选项卡查看详细档案。
  • 导数的概念及其几何意义
  • 等比数列的定义及性质
  • 一般数列的通项公式
  • 等比数列的前n项和
  • 反证法与放缩法

平均变化率:

一般地，对于函数y =f(x)，x1,x2是其定义域内不同的两点，那么函数的变化率可用式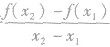表示，我们把这个式子称为函数f(x)从x1到x2的平均变化率，习惯上用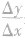表示，即平均变化率
  
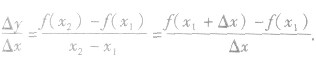
上式中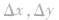的值可正可负，但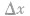不为0．f(x)为常数函数时，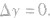 

瞬时速度:
如果物体的运动规律是s=s(t)，那么物体在时刻t的瞬时速度v就是物体在t到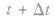这段时间内，当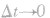时平均速度的极限，即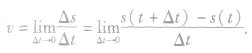
若物体的运动方程为s=f(t),那么物体在任意时刻t的瞬时速度v(t)就是平均速度v(t，d)为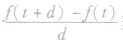当d趋于0时的极限．

函数y=f（x）在x=x0处的导数的定义：

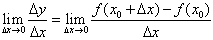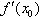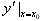一般地，函数y=f（x）在x=x0处的瞬时变化率是，我们称它为函数y=f（x）在x=x0处的导数，记作或，即。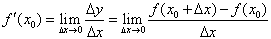

导函数：

如果函数y =f(x)在开区间(a，6)内的每一点都可导，则称在(a，b)内的值x为自变量，以x处的导数称为f(x为函数值的函数为fx）在(a，b)内的导函数，简称为f（x）在(a，b)内的导数，记作f′(x)或y′．即f′(x）=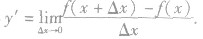

切线及导数的几何意义：

（1）切线：PPn为曲线f（x）的割线，当点Pn（xn，f（xn））（n∈N）沿曲线f（x）趋近于点P（x0，f（x0））时，割线PPn趋近于确定的位置，这个确定的位置的直线PT称为点P处的切线。
（2）导数的几何意义：函数f（x）在x=x0处的导数就是切线PT的斜率k，即k=。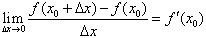


瞬时速度特别提醒：

①瞬时速度实质是平均速度当时的极限值．
②瞬时速度的计算必须先求出平均速度，再对平均速度取极限，

 函数y=f（x）在x=x0处的导数特别提醒：

①当时，比值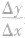的极限存在，则f（x）在点x0处可导；若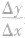的极限不存在，则f(x)在点x0处不可导或无导数．
②自变量的增量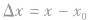可以为正，也可以为负，还可以时正时负，但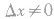．而函数的增量可正可负，也可以为0．
③在点x=x0处的导数的定义可变形为:
    

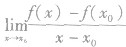
导函数的特点：

①导数的定义可变形为：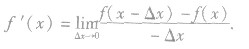
②可导的偶函数其导函数是奇函数，而可导的奇函数的导函数是偶函数，
③可导的周期函数其导函数仍为周期函数，
④并不是所有函数都有导函数．
⑤导函数与原来的函数f(x)有相同的定义域（a，b）,且导函数在x0处的函数值即为函数f(x)在点x0处的导数值．
⑥区间一般指开区间，因为在其端点处不一定有增量（右端点无增量，左端点无减量）．

导数的几何意义（即切线的斜率与方程）特别提醒：

①利用导数求曲线的切线方程．求出y=f(x)在x0处的导数f′(x)；利用直线方程的点斜式写出切线方程为y-y0 =f′(x0)（x- x0）．
②若函数在x= x0处可导，则图象在(x0，f(x0))处一定有切线，但若函数在x= x0处不可导，则图象在（x0，f(x0））处也可能有切线，即若曲线y =f(x)在点(x0，f(x0))处的导数不存在，但有切线，则切线与x轴垂直．
③注意区分曲线在P点处的切线和曲线过P点的切线，前者P点为切点；后者P点不一定为切点，P点可以是切点也可以不是，一般曲线的切线与曲线可以有两个以上的公共点，
④显然f′（x0）>0，切线与x轴正向的夹角为锐角；f′（x0）<o，切线与x轴正向的夹角为钝角；f(x0) =0，切线与x轴平行；f′(x0)不存在，切线与y轴平行．


等比数列的定义：

一般地，如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫做等比数列，这个常数叫做公比，公比通常用字母q表示（q≠0）。


等比数列的性质：

在等比数列｛an｝中，有
（1）若m+n=p+q，m，n，p，q∈N*，则aman=apaq；当m+n=2p时，aman=ap2；
（2）若m，n∈N*，则am=anqm-n；
（3）若公比为q，则｛｝是以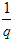为公比的等比数列；
（4）下标成等差数列的项构成等比数列；
（5）
1）若a1＞0，q＞1，则｛an｝为递增数列；
2）a1＜0，q＞1， 则｛an｝为递减数列；
3）a1＞0，0＜q＜1，则｛an｝为递减数列；
4）a1＜0， 0＜q＜1， 则｛an｝为递增数列；
5）q＜0，则｛an｝为摆动数列；若q＝1，则｛an｝为常数列。


等差数列和等比数列的比较：
 

如何证明一个数列是等比数列：

证明一个数列是等比数列，只需证明是一个与n无关的常数即可（或an2=an-1an+1）。


一般数列的定义：

如果数列{an}的第n项an与序号n之间的关系可以用一个式子表示成an=f（n），那么这个公式叫做这个数列的通项公式。


通项公式的求法：

（1）构造等比数列：凡是出现关于后项和前项的一次递推式都可以构造等比数列求通项公式；
（2）构造等差数列：递推式不能构造等比数列时，构造等差数列；
（3）递推：即按照后项和前项的对应规律，再往前项推写对应式。
已知递推公式求通项常见方法：
①已知a1=a,an+1=qan+b,求an时，利用待定系数法求解，其关键是确定待定系数λ，使an+1 +λ=q(an+λ)进而得到λ。
②已知a1=a,an=an-1+f(n)(n≥2),求an时，利用累加法求解，即an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)的方法。
③已知a1=a,an=f(n)an-1(n≥2)，求an时，利用累乘法求解。


等比数列的前n项和公式：

；


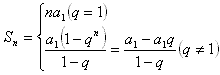等比数列中设元技巧：

已知a1，q，n，an ，Sn中的三个量，求其它两个量，是归结为解方程组问题，知三求二。
注意设元的技巧，如奇数个成等比数列，可设为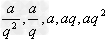：…，…（公比为q），但偶数个数成等比数列时，不能设为…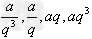，…因公比不一定为一个正数，公比为正时可如此设。

等比数列前n项和公式的变形：
q≠1时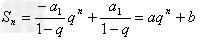，（a≠0，b≠0，a+b=0）；

等比数列前n项和常见结论：
一个等比数列有3n项，若前n项之和为S1，中间n项之和为S2，最后n项之和为S3，当q≠-1时，S1，S2，S3为等比数列。


反证法的定义：

有些不等式无法利用题设的已知条件直接证明，我们可以用间接的方法——反证法去证明，即通过否定原结论——导出矛盾——从而达到肯定原结论的目的。

放缩法的定义：

把原不等式放大或缩小成一个恰好可以化简的形式，比较常用的方法是把分母或分子适当放大或缩小（减去或加上一个正数）使不等式简化易证。


反证法证题的步骤：

若A成立，求证B成立。
共分三步：
（1）提出与结论相反的假设；如负数的反面是非负数，正数的反面是非正数即0和负数；
（2）从假设出发，经过推理，得出矛盾；（必须由假设出发进行推理否则不是反证法或证错）；
（3）由矛盾判定假设不正确，从而肯定命题的结论正确.矛盾：与定义、公理、定理、公式、性质等一切已有的结论矛盾甚至自相矛盾。
反证法是一种间接证明命题的基本方法。在证明一个数学命题时，如果运用直接证明法比较困难或难以证明时，可运用反证法进行证明。

放缩法的意义：

放缩法理论依据是不等式的传递性：若,a<b,b<c，则a<c.

放缩法的操作：

若求证P<Q，先证P<P1<P2<…<Pn,再证恰有Pn<Q.
需注意：（1）只有同方向才可以放缩，反方向不可。
（2）不能放（缩）得太大（小），否则不会有最后的Pn<Q.


发现相似题
与“已知函数f（x）=x2-4，设曲线y=f（x）在点（xn，f（xn））处...”考查相似的试题有：